7.1 Leçon
Au module 4, vous avez appris les fonctions essentielles pour lire et visualiser des données spatiales vectorielles sous R. Le présent module vous amènera maintenant à manipuler des données vectorielles.
Dans un premier temps, cette leçon vous enseignera le fonctionnement d’opérations de base sur les données vectorielles. Ces opérations comprennent deux grandes catégories: les opérations qui portent sur les attributs des données vectorielles et les opérations qui portent sur la géométrie des données vectorielles. Les opérations réalisées sur les attributs des données vectorielles sont indépendantes de la composante spatiale des données, alors que les opérations spatiales prennent en considération la géométrie des données et peuvent même la transformer.
Dans un second temps, cette leçon vous guidera dans la résolution d’une problématique qui nécessite de manipuler des données vectorielles. Au cours des différentes étapes permettant de résoudre la problématique, vous mettrez en pratique les diverses fonctions R apprises jusqu’à maintenant. Plus précisément, nous allons explorer le territoire Québécois en nous posant la question suivante:
Parmi les dix plus grandes villes du Québec, quelle est celle qui dispose du plus grand nombre de parcs nationaux dans un rayon de 70 km ?
7.1.1 Télécharger les données
Dans cette leçon, nous allons utiliser les données vectorielles relatives aux municipalités et aux régions administratives du Québec, ainsi qu’au réseau de la Société des établissements de plein air du Québec, la SÉPAQ.
Afin de faciliter le téléchargement de ces données, l’ensemble de ces couches d’informations spatiales peut être téléchargé en cliquant sur un seul lien: données pour le module 7.
Sauvegardez le dossier compressé (zip) dans votre répertoire de travail Module7_donnees pour ce module, et dézippez-le. Le dossier comprend trois sous-dossiers et un fichier .csv:
villes,parcs.gdb,regions_admin,population.csv.
7.1.2 Opérations de base
7.1.2.1 Importer et visualiser les données
Commençons par charger les bibliothèques requises pour lire les données spatiales vectorielles (sf) et les visualiser (mapview).
library(sf)
library(mapview)Maintenant, allons lire le fichier shapefile de l’ensemble des municipalités du Québec en utilisant la fonction st_read() tel que vu dans le module 4.
municipalites <- st_read("Module7/Module7_donnees/villes/villes.shp")Reading layer `villes' from data source
`D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module7\Module7_donnees\villes\villes.shp'
using driver `ESRI Shapefile'
Simple feature collection with 767 features and 17 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate SystemLe shapefile a été importé dans un objet R de classe sf (c’est-à-dire un objet importé ou généré par l’utilisation de la bibliothèque sf). Nous remarquons que la géométrie de cet object vectoriel est de type point (POINT). Plus précisément, cet objet contient 767 points (features) et 17 attributs (fields).
Pour en savoir davantage sur ces attributs de nature géographique, démographique et administrative, vous pouvez télécharger et consulter la [documentation] (https://www.donneesquebec.ca/recherche/fr/dataset/base-de-donnees-geographiques-et-administratives/resource/beb4472a-0edb-4824-b67e-40e20b425326) disponible sur le site de Données Québec.
Nous pouvons maintenant visuellement valider que l’importation des données a bien été réussie en utilisant la fonction mapview() :
mapview(municipalites, legend = FALSE) Dans le précédent module portant sur la cartographie, nous avons décrit plusieurs fonctionnalités de la bibliothèque tmap et avons démontré sa flexibilité et sa capacité à produire des cartes de grande qualité. Toutefois, la bibliothèque mapview demeure fort utile lorsque nous souhaitons visualiser rapidement des données. Par défaut, la fonction mapview() affiche la carte d’OpenstreeMap en arrière-pan, ce qui permet de contextualiser facilement les données.
De plus, les cartes produites avec mapview() sont interactives, permettant d’accéder directement à la table d’attributs des données vectorielles représentées. Par exemple, sur la carte ci-dessus, vous n’avez qu’à cliquer sur le marqueur géographique correspondant à chaque municipalité (point) ou à chaque parc (polygone) pour obtenir la liste des attributs et leur valeur. De plus, vous pouvez choisir d’afficher l’une ou l’autre des couches en cochant la couche désirée dans la fenêtre située dans le coin supérieur gauche.
7.1.2.2 Opérations sur les attributs des données vectorielles
Les opérations sur les données vectorielles peuvent être séparées en deux grandes catégories. Les opérations qui portent sur les attributs des données et les opérations qui portent sur la géométrie des données.
Les opérations réalisées sur les attributs des données vectorielles sont indépendantes de la composante spatiale des données. Ce sont des fonctions générales pour manipuler des bases de données et qui s’appliquent aux data.frame des données vectorielles. La présente section s’attarde à décrire certaines de ces fonctions.
Filter des attributs
Une opération fréquente lorsque nous manipulons des données vectorielles est celle de filtrer les données. Par exemple, dans le shapefile municipalites que nous venons d’importer, nous pourrions vouloir sélectionner seulement certaines municipalités parmi les 767 répertoriées ou certains attributs parmi les 17. Nous pourrions aussi vouloir déterminer quelles municipalités possèdent une valeur spécifique pour un attribut donné.
Dans les sous-sections qui suivent, nous présenterons des opérations qui permettent de filtrer les attributs de données vectorielles.
Sélectionner des attributs à partir de leur indice
Les objets sf sont manipulables de la même façon qu’un data.frame (étant eux-mêmes des data.frame). Les attributs correspondent aux colonnes tandis que les entités spatiales (points, lignes ou polygones) correspondent aux lignes du data.frame.
Par exemple, l’objet spatial municipalites contient 767 points correspondant chacun à une municipalité. La table d’attributs contient quant à elle 18 colonnes correspondant à chacun des attributs permettant de décrire les municipalités.
Pour sélectionner un élément spatial spécifique d’un shapefile, nous pouvons simplement spécifier l’indice de la ligne qui lui est associée dans le data.frame. Par exemple :
municipalites[1, ] # Pour accéder à la première ligne. Simple feature collection with 1 feature and 17 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -57.13 ymin: 51.43 xmax: -57.13 ymax: 51.43
Geodetic CRS: Geographic Coordinate System
LAYER AREA PERIMETER HABIT_P.
1 Unknown Point Feature 0 0 1
HABIT_P_ID HABIT_P_ HABIT_P_I1 HAP_CO_PRE
1 1 1 417 PRE
HAP_NO_IND HAP_DE_IND HAP_CO_CLA HAP_CO_TOP
1 03 63 0000 001 Lieu habité TER 236021
HAP_NM_TOP HAP_DA_TOP HAP_CO_VER HAP_DA_MOD
1 Blanc-Sablon 20010115 BDGA1M v1.1 0
INT_AFF geometry
1 2M POINT (-57.13 51.43)Nous remarquons que le nombre de features (points) est maintenant de 1 (voir la première ligne de la sortie produite par R). En effet, puisque nous avons sélectionné le premier point de l’objet spatial municipalites nous avons exclu les 766 autres points.
De la même manière, pour sélectionner un attribut spécifique, nous pouvons simplement spécifier l’indice de la colonne qui lui est associée :
municipalites[, 2] # Pour accéder à la deuxième colonne. Simple feature collection with 767 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate System
First 10 features:
AREA geometry
1 0 POINT (-57.13 51.43)
2 0 POINT (-57.2 51.41)
3 0 POINT (-76.25 51.69)
4 0 POINT (-78.75 51.49)
5 0 POINT (-58.65 51.23)
6 0 POINT (-59.62 50.47)
7 0 POINT (-73.87 50.41)
8 0 POINT (-60.67 50.22)
9 0 POINT (-62.81 50.29)
10 0 POINT (-64.33 50.29)Nous remarquons également que le nombre de fields (colonnes) a diminué à 1.
Sélectionner des attributs à partir de leur nom
Il est également possible de sélectionner un attribut particulier en spécifiant son nom.
Les colonnes disposent toujours d’un nom unique dans un data.frame. Nous pouvons afficher le nom des colonnes en utilisant la fonction names() :
names(municipalites) [1] "LAYER" "AREA" "PERIMETER"
[4] "HABIT_P." "HABIT_P_ID" "HABIT_P_"
[7] "HABIT_P_I1" "HAP_CO_PRE" "HAP_NO_IND"
[10] "HAP_DE_IND" "HAP_CO_CLA" "HAP_CO_TOP"
[13] "HAP_NM_TOP" "HAP_DA_TOP" "HAP_CO_VER"
[16] "HAP_DA_MOD" "INT_AFF" "geometry" Cette table contient 17 attributs. L’attribut nommé HAP_NM_TOP réfère au nom des municipalités. Notez que l’abréviation TOP signifie toponyme.
Pour sélectionner cet attribut nous pouvons le faire simplement en utilisant son nom. Par exemple, en utilisant la syntaxe suivante :
municipalites[, "HAP_NM_TOP"]Simple feature collection with 767 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate System
First 10 features:
HAP_NM_TOP geometry
1 Blanc-Sablon POINT (-57.13 51.43)
2 Lourdes-de-Blanc-Sablon POINT (-57.2 51.41)
3 Nemiscau POINT (-76.25 51.69)
4 Waskaganish POINT (-78.75 51.49)
5 Saint-Augustin POINT (-58.65 51.23)
6 Chevery POINT (-59.62 50.47)
7 Mistissini POINT (-73.87 50.41)
8 La Romaine POINT (-60.67 50.22)
9 Baie-Johan-Beetz POINT (-62.81 50.29)
10 Rivière-Saint-Jean POINT (-64.33 50.29)# Ce qui revient également au même que la syntaxe suivante
municipalites[, 13] Simple feature collection with 767 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate System
First 10 features:
HAP_NM_TOP geometry
1 Blanc-Sablon POINT (-57.13 51.43)
2 Lourdes-de-Blanc-Sablon POINT (-57.2 51.41)
3 Nemiscau POINT (-76.25 51.69)
4 Waskaganish POINT (-78.75 51.49)
5 Saint-Augustin POINT (-58.65 51.23)
6 Chevery POINT (-59.62 50.47)
7 Mistissini POINT (-73.87 50.41)
8 La Romaine POINT (-60.67 50.22)
9 Baie-Johan-Beetz POINT (-62.81 50.29)
10 Rivière-Saint-Jean POINT (-64.33 50.29)# Puisque cette colonne est en treizième position.Notez que la syntaxe familière municipalites$HAP_NM_TOP retourne un vecteur listant les valeurs de l’attribut HAP_NM_TOP, mais ne conserve pas la géométrie du shapefile:
head(municipalites$HAP_NM_TOP)[1] "Blanc-Sablon" "Lourdes-de-Blanc-Sablon"
[3] "Nemiscau" "Waskaganish"
[5] "Saint-Augustin" "Chevery" Toutefois, la syntaxe précédente conserve la géométrie du shapefile et peut ainsi être utilisée pour définir un nouvel objet spatial. Par exemple, créons un nouveau shapefile qui contient seulement le nom des municipalités et leur position géographique :
villes <- municipalites[,"HAP_NM_TOP"]
villesSimple feature collection with 767 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate System
First 10 features:
HAP_NM_TOP geometry
1 Blanc-Sablon POINT (-57.13 51.43)
2 Lourdes-de-Blanc-Sablon POINT (-57.2 51.41)
3 Nemiscau POINT (-76.25 51.69)
4 Waskaganish POINT (-78.75 51.49)
5 Saint-Augustin POINT (-58.65 51.23)
6 Chevery POINT (-59.62 50.47)
7 Mistissini POINT (-73.87 50.41)
8 La Romaine POINT (-60.67 50.22)
9 Baie-Johan-Beetz POINT (-62.81 50.29)
10 Rivière-Saint-Jean POINT (-64.33 50.29)Profitons-en pour renommer l’attribut HAP_NM_TOP afin d’avoir un intitulé de colonne plus explicite :
names(villes) <- c("toponyme", "geometry")
names(villes)[1] "toponyme" "geometry"Filtrer des valeurs d’attribut
On peut vouloir sélectionner un ou plusieurs éléments spatiaux d’un shapefile qui possèdent une valeur spécifique d’attribut. Cette opération peut être réalisée en utilisant les fonctions subset() ou which().
Fonction subset()
La fonction subset() n’est pas spécifique aux données spatiales, c’est une fonction générale de R qui retourne le sous-ensemble d’un vecteur, d’une matrice or d’un tableau de données qui satisfait une condition donnée.
Par exemple, nous pouvons utiliser la fonction subset() pour filtrer le jeu de données villes afin d’obtenir la localisation d’une municipalité précise:
la_poc <- subset(villes, toponyme == "La Pocatière")
mapview(la_poc, legend = FALSE)Notez que l’objet retourné, ici la_poc, est de même classe que l’objet filtré, ici villes. Nous pouvons valider la classe d’un objet dans R avec la fonction class().
class(la_poc)[1] "sf" "data.frame"Fonction which()
La fonction which() est aussi une fonction générale de R. Elle identifie la position des éléments de valeur TRUE dans un vecteur logique. Par exemple:
#Exemple 1
which(c(TRUE, FALSE, TRUE, FALSE, TRUE))[1] 1 3 5#Exemple 2
which(c(1, 1, 2) == 2)[1] 3Maintenant, utilisons la fonction which() pour isoler la ville de La Pocatière:
which(villes$toponyme == "La Pocatière")[1] 128Remarquez que la fonction which() retourne l’indice de la ligne dans la table d’attributs de l’objet villes satisfaisant la condition toponyme == "La Pocatière".
Nous pouvons ensuite consigner cet identifiant dans l’objet id_la_poc et l’utiliser pour déterminer la localisation de la ville de La Pocatière:
id_la_poc <- which(villes$toponyme == "La Pocatière")
villes[id_la_poc,] Simple feature collection with 1 feature and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -70.04 ymin: 47.37 xmax: -70.04 ymax: 47.37
Geodetic CRS: Geographic Coordinate System
toponyme geometry
128 La Pocatière POINT (-70.04 47.37)Ajouter des attributs
Un autre type de manipulations fréquemment utilisé est celui d’enrichir un jeu de données vectorielles en lui ajoutant des attributs. Ces nouvelles informations peuvent provenir d’une base de données non-spatiales ou d’un autre shapefile.
Dans le cas de données non-spatiales, nous pouvons combiner les attributs désirés en utilisant l’opération merge() que nous définissons dans cette sous-section. Lorsque nous souhaitons ajouter des attributs provenant de données spatiales, nous devons faire une jointure spatiale en utilisant l’opération st_join(). Nous définirons st_join() dans la section suivante portant sur les opérations spatiales sur les données vectorielles.
La fonction merge()
La fonction merge() est une fonction générale de R qui sert à combiner deux tableaux de données différents en se servant de rangées ou de colonnes communes.
Par exemple, ajoutons à chacune des municipilatés contenues dans le shapefile villes la taille de sa population. Cette information est contenue dans un fichier csv (Module7_donnees/ville/population.csv) et provient du répertoire des municipalités du Québec.
Nous allons d’abord importer ce fichier CSV dans R en utilisant la fonction read.csv(). Ensuite, nous sélectionnerons les colonnes pertinentes de ce tableau, et nous ajouterons ces informations aux attributs de l’objet spatial villes.
pop <- read.csv("Module7/Module7_donnees/villes/population.csv",encoding="UTF-8")Notez que la précision de l’encodage assure que les accents français sont bien importés lors de la lecture du document.
L’objet pop est un data.frame de 114 colonnes décrivant un ensemble d’informations propres aux municipalités du Québec allant de leur nom jusqu’à la composition de leur conseil municipal. Toutes ces informations ne sont pas pertinentes pour le présent exercice. Pour faciliter la manipulation de ce tableau, sélectionnons seulement les colonnes suivantes:
munnom: Nom de la ville.msuperf: Superficie de la municipalité.mpopul: Taille de la population de la municipalité.
pop <- pop[, c("munnom", "msuperf", "mpopul")]Le nouvel objet pop ainsi défini, contient seulement 3 colonnes.
Nous voulons à présent fusionner l’objet pop avec l’objet spatial villes en utilisant la fonction merge(). Cette fusion entre les deux objets villes et pop sera réalisée sur les colonnes toponyme et munnom respectivement. Ces deux colonnes contiennent le nom des municipalités et agissent donc comme dénominateur commun entre les deux jeux de données.
#villes_qc <- merge(x = villes_qc, y = pop, by.x="toponyme", by.y="munnom", all.x = TRUE)
villes_pop <- merge(x = villes, y = pop, by.x="toponyme", by.y="munnom")
villes_popSimple feature collection with 485 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -82.93 ymin: 42.31 xmax: -56.18 ymax: 62.42
Geodetic CRS: Geographic Coordinate System
First 10 features:
toponyme msuperf mpopul geometry
1 Acton Vale 91.1 7733 POINT (-72.56 45.65)
2 Aguanish 680.6 238 POINT (-62.08 50.22)
3 Akulivik 82.3 678 POINT (-78.2 60.81)
4 Albanel 205.0 2232 POINT (-72.44 48.88)
5 Alma 232.6 30831 POINT (-71.65 48.54)
6 Amherst 249.5 1459 POINT (-64.21 45.83)
7 Amos 437.2 12769 POINT (-78.12 48.57)
8 Amqui 128.3 6065 POINT (-67.43 48.46)
9 Armagh 170.6 1502 POINT (-70.59 46.74)
10 Asbestos 31.8 6837 POINT (-71.93 45.77)Le nouveau shapefile villes_pop contient les mêmes attributs que villes auxquels se sont ajoutés les attributs de pop.
Remarquez que villes_pop contient moins d’éléments que villes. En effet, la fonction merge() n’a retenue que les villes qui étaient contenues à la fois dans le shapefile villes et dans la base de données pop. Pour conserver l’entièreté des éléments initialement présents dans villes, il faudrait ajouter l’argument all.x = TRUE à la fonction merge(). Dans ce cas, les villes dont la population n’est pas définie dans pop se verraient attribuer une valeur NA à l’attribut mpopul.
Renommons les colonnes de villes_pop pour qu’elles portent un nom plus représentatif de leur contenu.
names(villes_pop)[1] "toponyme" "msuperf" "mpopul" "geometry"names(villes_pop)[2:3] <- c("superficie", "population")
names(villes_pop) [1] "toponyme" "superficie" "population" "geometry" 7.1.2.3 Opérations spatiales sur les données vectorielles
Les opérations réalisées dans la section précédente sur les attributs des données vectorielles, telles merge(), which() et subset(), sont indépendantes de la composante spatiale des données. Si nous changions la géométrie des objets spatiaux décrits par les données vectorielles (par exemple en changeant les coordonnées des villes), ces opérations produiraient les mêmes résultats. Ce sont des fonctions générales pour manipuler des bases de données et qui s’appliquent aux data.frame des données vectorielles.
Dans la présente section, nous verrons plutôt des opérations qui dépendent de la composante spatiale des données vectorielles. Ces opérations prennent en considération la géométrie des données et certaines peuvent aussi la transformer.
Jointure spatiale
Une opération de jointure permet de lier entre eux des éléments spatiaux sur la base d’une valeur d’attribut commune.
La fonction st_join()
La fonction st_join() de la bibliothèque sf permet de joindre à un shapefile de l’information provenant d’une autre couche spatiale. Cette opération constitue une jointure spatiale.
Par exemple, importons le shapefile des régions administratives du Québec, disponible dans le dossier Module7_données, et réalisons une jointure entre cette couche et la couche villes.
regions <- st_read("Module7/Module7_donnees/regions_admin/regions_admin.shp")Reading layer `regions_admin' from data source
`D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module7\Module7_donnees\regions_admin\regions_admin.shp'
using driver `ESRI Shapefile'
Simple feature collection with 21 features and 1 field
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System# on observe le contenu de ce shaphefile
regionsSimple feature collection with 21 features and 1 field
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
Rgns_Ad
1 Côte-Nord
2 Côte-Nord
3 Côte-Nord
4 Saguenay - Lac-Saint-Jean
5 Gaspésie - Îles-de-la-Madeleine
6 Bas-Saint-Laurent
7 Abitibi-Témiscamingue
8 Mauricie
9 Capitale-Nationale
10 Outaouais
geometry
1 POLYGON ((-66.69 55, -66.64...
2 POLYGON ((-66.26 55, -66.25...
3 POLYGON ((-67.22 55, -67 55...
4 POLYGON ((-72.07 47.95, -72...
5 POLYGON ((-67.15 49.19, -67...
6 POLYGON ((-67.15 49.19, -66...
7 POLYGON ((-75.52 47.85, -75...
8 POLYGON ((-74.47 48.95, -74...
9 POLYGON ((-72.07 47.95, -72...
10 POLYGON ((-75.52 47.85, -75...# on le visualise
mapview(regions)Notez que les éléments de regions sont des polygones. Ces polygones possèdent un seul attribut, "Rgns_Ad", correspondant au nom des régions administratives que ceux-ci délimitent.
Nous allons maintenant faire une jointure spatiale entre villes et regions afin d’associer à chaque municipalité sa région administrative d’attache.
villes_reg = st_join(villes, regions[ ,"Rgns_Ad"])
villes_regSimple feature collection with 767 features and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -83.64 ymin: 42.05 xmax: -51.73 ymax: 64.19
Geodetic CRS: Geographic Coordinate System
First 10 features:
toponyme Rgns_Ad
1 Blanc-Sablon Côte-Nord
2 Lourdes-de-Blanc-Sablon Côte-Nord
3 Nemiscau Nord-du-Québec
4 Waskaganish Nord-du-Québec
5 Saint-Augustin Côte-Nord
6 Chevery Côte-Nord
7 Mistissini Nord-du-Québec
8 La Romaine Côte-Nord
9 Baie-Johan-Beetz Côte-Nord
10 Rivière-Saint-Jean Côte-Nord
geometry
1 POINT (-57.13 51.43)
2 POINT (-57.2 51.41)
3 POINT (-76.25 51.69)
4 POINT (-78.75 51.49)
5 POINT (-58.65 51.23)
6 POINT (-59.62 50.47)
7 POINT (-73.87 50.41)
8 POINT (-60.67 50.22)
9 POINT (-62.81 50.29)
10 POINT (-64.33 50.29)Remarquez que l’objet villes_reg est identique à l’objet villes mais contient un attribut supplémentaire: la colonne Rgns_Ad.
Il est important de préciser que la fonction st_join() nécessite que les deux couches spatiales à joindre utilisent le même système de coordonnées de référence (SCR).
Contrairement à la fonction merge() vue plus haut, la fonction st_join() est bien une opération spatiale. En effet, st_join(x,y) détermine s’il y a une intersection spatiale entre chaque élément de l’objet de gauche (x = villes) et l’un ou l’autre des éléments de l’objet de droite (y = regions). Une intersection entre deux éléments spatiaux se produit lorsqu’ils partagent une même portion de l’espace. Ainsi, il y a une intersection entre le point associé à la ville de Shawinigan et le polygone associé à la région de la Mauricie. Par ailleurs, il n’y a pas d’intersection entre le point associé à la ville de Sherbrooke et le polygone de la Mauricie.
Lorsque st_join(x,y) identifie la présence d’une intersection entre deux éléments, elle assigne à l’élément de gauche la valeur de l’attribut (ici "Rgns_Ad") de l’élément de droite.
Lorsqu’il n’y a pas d’intersection entre deux éléments, la fonction assigne une valeur d’attribut NA à l’élément de gauche. Par exemple, les données villes contiennent des municipalités qui ne sont pas situées au Québec. On retrouve entre autres la ville d’Albany dans l’état de New York aux États-Unis. Ainsi aucune région n’a pu être associée à ces villes.
villes_reg[692,]Simple feature collection with 1 feature and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -73.77 ymin: 42.66 xmax: -73.77 ymax: 42.66
Geodetic CRS: Geographic Coordinate System
toponyme Rgns_Ad geometry
692 Albany <NA> POINT (-73.77 42.66)Si nous souhaitons que la fonction st_join(x,y) conserve seulement les éléments de x qui intersectent un ou l’autre des éléments de y, nous devons ajouter l’argument left = FALSE :
villes_reg <- st_join(villes, regions[ ,"Rgns_Ad"], left = FALSE)Visualisons le nouveau shapefile que nous venons de créer. Ce dernier contient seulement les municipalités à l’intérieur du territoire québécois.
mapview(villes_reg, legend = FALSE)Notez que lorsque vous cliquez sur les points de la carte, la valeur de l’attribut “Rngs_Ad” est maintenant également donnée.
Vous pouvez ainsi différencier visuellement les municipalités selon leur région administrative d’attache.
mapview(villes_reg, zcol = "Rgns_Ad", legend = FALSE)Que se produit-il si nous inversons les arguments villes et regions dans la fonction st-join() ? Dans ce cas, la jointure spatiale associe à chaque région les villes qui sont situées (c’est-à-dire intersectent) son territoire. Observons le résultat d’une telle jointure :
reg_villes <- st_join(regions, villes[,"toponyme"], left = FALSE)
reg_villesSimple feature collection with 620 features and 2 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -57.11 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
Rgns_Ad toponyme
3 Côte-Nord Kawawachikamach
3.1 Côte-Nord Matimekosh
3.2 Côte-Nord Schefferville
4 Saguenay - Lac-Saint-Jean Girardville
4.1 Saguenay - Lac-Saint-Jean Albanel
4.2 Saguenay - Lac-Saint-Jean Mistassini
4.3 Saguenay - Lac-Saint-Jean Dolbeau
4.4 Saguenay - Lac-Saint-Jean Normandin
4.5 Saguenay - Lac-Saint-Jean Sainte-Monique
4.6 Saguenay - Lac-Saint-Jean La Doré
geometry
3 POLYGON ((-67.22 55, -67 55...
3.1 POLYGON ((-67.22 55, -67 55...
3.2 POLYGON ((-67.22 55, -67 55...
4 POLYGON ((-72.07 47.95, -72...
4.1 POLYGON ((-72.07 47.95, -72...
4.2 POLYGON ((-72.07 47.95, -72...
4.3 POLYGON ((-72.07 47.95, -72...
4.4 POLYGON ((-72.07 47.95, -72...
4.5 POLYGON ((-72.07 47.95, -72...
4.6 POLYGON ((-72.07 47.95, -72...Le shapefile reg_villes est constitué des polygones de regions. Puisque plusieurs municipalités intersectent chaque région, le polygone d’une région donnée est dupliqué pour chacun des points. C’est-à-dire qu’une nouvelle ligne est ajoutée pour chacune des intersections identifiées.
Remarquez que nous pouvons aussi utiliser la fonction join_st() en vue de créer un filtre spatial, par exemple avec la fonction subset() :
villes_CN<- subset(villes_reg, Rgns_Ad=="Côte-Nord")
mapview(villes_CN, legend = FALSE)Cette opération nous a permis de filtrer les municipalités du Québec pour retenir seulement celles situées dans la région administrative de la Côte-Nord.
Opérations géométriques
Les opérations géométriques sur les données vectorielles sont des opérations qui peuvent changer la géométrie des données ou qui peuvent créer, à partir de celles-ci, de nouveaux objets vectoriels de géométrie différente.
La fonction aggregate()
La fonction aggregate() de la bibliothèque sf permet d’agréger (c’est-à-dire de grouper) des éléments spatiaux d’une même couche de données vectorielles.
Afin de démontrer comment opère la fonction aggregate(), considérons d’abord l’objet villes_reg_pop. Ce dernier est formé par la jointure spatiale entre villes_pop, le shapefile associant à chaque municipalité la taille de sa population, et regions :
villes_reg_pop <- st_join(villes_pop, regions[ ,"Rgns_Ad"], left = FALSE)
villes_reg_popSimple feature collection with 477 features and 4 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -79.5 ymin: 45.05 xmax: -57.13 ymax: 62.42
Geodetic CRS: Geographic Coordinate System
First 10 features:
toponyme superficie population
1 Acton Vale 91.1 7733
2 Aguanish 680.6 238
3 Akulivik 82.3 678
4 Albanel 205.0 2232
5 Alma 232.6 30831
7 Amos 437.2 12769
8 Amqui 128.3 6065
9 Armagh 170.6 1502
10 Asbestos 31.8 6837
11 Aupaluk 32.7 224
Rgns_Ad geometry
1 Montérégie POINT (-72.56 45.65)
2 Côte-Nord POINT (-62.08 50.22)
3 Nord-du-Québec POINT (-78.2 60.81)
4 Saguenay - Lac-Saint-Jean POINT (-72.44 48.88)
5 Saguenay - Lac-Saint-Jean POINT (-71.65 48.54)
7 Abitibi-Témiscamingue POINT (-78.12 48.57)
8 Bas-Saint-Laurent POINT (-67.43 48.46)
9 Chaudière-Appalaches POINT (-70.59 46.74)
10 Estrie POINT (-71.93 45.77)
11 Nord-du-Québec POINT (-69.61 59.3)L’objet villes_reg_pop associe à chaque municipalité la taille de sa population ainsi que sa région administrative.
En agrégeant ensemble les villes d’une même région, il nous est possible de déterminer la taille de la population de cette région. C’est ce que nous allons faire en utilisant la fonction aggregate() :
reg_pop<-aggregate(villes_reg_pop["population"], by = list(villes_reg_pop$Rgns_Ad), FUN = sum, na.rm = TRUE)
reg_popSimple feature collection with 17 features and 2 fields
Attribute-geometry relationships: aggregate (1), identity (1)
Geometry type: GEOMETRY
Dimension: XY
Bounding box: xmin: -79.5 ymin: 45.05 xmax: -57.13 ymax: 62.42
Geodetic CRS: Geographic Coordinate System
First 10 features:
Group.1 population
1 Abitibi-Témiscamingue 125833
2 Bas-Saint-Laurent 143428
3 Capitale-Nationale 684340
4 Centre-du-Québec 201807
5 Chaudière-Appalaches 372758
6 Côte-Nord 72674
7 Estrie 251011
8 Gaspésie - Îles-de-la-Madeleine 62017
9 Lanaudière 409733
10 Laurentides 388382
geometry
1 MULTIPOINT ((-79.5 48.87), ...
2 MULTIPOINT ((-70.04 47.37),...
3 MULTIPOINT ((-72.27 46.76),...
4 MULTIPOINT ((-72.82 46.06),...
5 MULTIPOINT ((-72 46.57), (-...
6 MULTIPOINT ((-69.8 48.24), ...
7 MULTIPOINT ((-72.31 45.49),...
8 MULTIPOINT ((-66.69 49.1), ...
9 MULTIPOINT ((-73.92 46.68),...
10 MULTIPOINT ((-75.62 46.09),...De façon générale, la fonction aggregate(x, by, FUN) comprend trois arguments:
xest l’objet spatial que l’on souhaite agréger,bydéfini la condition utilisée pour regrouper les éléments dex,FUNdéfini la fonction selon laquelle l’attribut d’un groupement est calculé à partir des attributs des éléments agrégés.
Dans notre exemple, nous avons regroupé les points de l’objet spatial villes_reg_pop["population"] qui possèdent la même valeur d’attribut "Rgns_Ad". Les points ainsi regroupés forment une géométrie multipoint (MULTIPOINT). Chaque groupe de points est identifié par le nom de sa région administrative (Abitibi-Témiscamingue, Bas-Saint-Laurent, etc.). L’attribut d’un groupe est calculé en faisant la somme (FUN = sum) des attributs des points qui le constituent. L’argument additionnel na.rm = TRUE précise que lors du calcul de la somme, les éléments dont l’attribut "population" prend la valeur NA doivent être ignorés. En effet, la population de quelques municipalités n’est pas définie dans cette base de données. Notez qu’une autre fonction aurait pu être utilisée, par exemple la moyenne, le maximum, le minimum, etc.
La condition by peut prendre différentes formes. Elle peut être définie par une liste de longueur égale au nombre d’éléments dans x (c’est-à-dire le même nombre de rangées). C’est de cette façon que nous l’avons définie plus haut (la liste est de longueur égale aux nombres de points dans villes_reg_pop). De plus, by peut prendre la forme d’un objet spatial dont la géométrie est utilisée pour grouper les éléments de x. Dans ce cas, la géométrie du nouvel objet créé par la fonction aggregate() est la même que l’objet by.
Donnons un exemple illustrant cette situation. Agrégeons maintenant les municipalités de l’objet villes_pop["population"] en utilisant directement l’objet regions constitué de polygones :
reg_pop2 <-aggregate(villes_pop["population"], by = regions, FUN = sum, na.rm = TRUE)
reg_pop2Simple feature collection with 21 features and 1 field
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
population geometry
1 NA POLYGON ((-66.69 55, -66.64...
2 NA POLYGON ((-66.26 55, -66.25...
3 157 POLYGON ((-67.22 55, -67 55...
4 91339 POLYGON ((-72.07 47.95, -72...
5 62017 POLYGON ((-67.15 49.19, -67...
6 143428 POLYGON ((-67.15 49.19, -66...
7 125833 POLYGON ((-75.52 47.85, -75...
8 275487 POLYGON ((-74.47 48.95, -74...
9 684340 POLYGON ((-72.07 47.95, -72...
10 311130 POLYGON ((-75.52 47.85, -75...Observez que les groupements sont maintenant des polygones, et non des multipoints. Par ailleurs le calcul de l’attribut "population" est le même.
Une visualisation du nouvel objet reg_pop2 permet d’illustrer les régions selon la taille de leur population :
mapview(reg_pop2)Donnons un dernier exemple de l’utilisation de la fonction aggregate() en considérant le shapefile régions
regionsSimple feature collection with 21 features and 1 field
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
Rgns_Ad
1 Côte-Nord
2 Côte-Nord
3 Côte-Nord
4 Saguenay - Lac-Saint-Jean
5 Gaspésie - Îles-de-la-Madeleine
6 Bas-Saint-Laurent
7 Abitibi-Témiscamingue
8 Mauricie
9 Capitale-Nationale
10 Outaouais
geometry
1 POLYGON ((-66.69 55, -66.64...
2 POLYGON ((-66.26 55, -66.25...
3 POLYGON ((-67.22 55, -67 55...
4 POLYGON ((-72.07 47.95, -72...
5 POLYGON ((-67.15 49.19, -67...
6 POLYGON ((-67.15 49.19, -66...
7 POLYGON ((-75.52 47.85, -75...
8 POLYGON ((-74.47 48.95, -74...
9 POLYGON ((-72.07 47.95, -72...
10 POLYGON ((-75.52 47.85, -75...Remarquez que certaines régions, comme la Côte-Nord, sont représentées par plusieurs polygones. C’est pour cette raison que ce shapefile contient 21 éléments spatiaux alors qu’il y a 17 régions administratives au Québec.
Utilisons la fonction aggregate() pour agréger en un seul multipolygone les polygones qui portent la même valeur d’attribut "Rgns_Ad" :
regions_agg <-aggregate(regions, by=list(regions$Rgns_Ad), unique)
regions_aggSimple feature collection with 17 features and 2 fields
Attribute-geometry relationships: aggregate (1), identity (1)
Geometry type: GEOMETRY
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
Group.1
1 Abitibi-Témiscamingue
2 Bas-Saint-Laurent
3 Capitale-Nationale
4 Centre-du-Québec
5 Chaudière-Appalaches
6 Côte-Nord
7 Estrie
8 Gaspésie - Îles-de-la-Madeleine
9 Lanaudière
10 Laurentides
Rgns_Ad
1 Abitibi-Témiscamingue
2 Bas-Saint-Laurent
3 Capitale-Nationale
4 Centre-du-Québec
5 Chaudière-Appalaches
6 Côte-Nord
7 Estrie
8 Gaspésie - Îles-de-la-Madeleine
9 Lanaudière
10 Laurentides
geometry
1 POLYGON ((-75.52 47.85, -75...
2 POLYGON ((-67.15 49.19, -66...
3 POLYGON ((-72.07 47.95, -72...
4 POLYGON ((-72.08 46.57, -72...
5 POLYGON ((-70.2 47.41, -70....
6 MULTIPOLYGON (((-67.41 54.9...
7 POLYGON ((-71.46 45.82, -71...
8 POLYGON ((-67.15 49.19, -67...
9 POLYGON ((-74.89 47.76, -74...
10 POLYGON ((-75.52 47.76, -75...Cette fois nous avons utilisé la fonction unique pour agréger les attributs qui sont de classe caractère. Remarquez que la Côte-Nord est maintenant représentée par un multipolygone (MULTIPOLYGON) et que le nouveau shapefile regions_agg contient 17 éléments, un pour chacune des régions administratives.
Retirons la première colonne superflue de ce nouveau shapefile et utilisons-le dans les futurs exemples pour désigner les régions administratives.
regions <- regions_agg[-1] #pour retirer la première colonneLa fonction st_simplify()
Il est parfois utile de simplifier les objets vectoriels de types ligne ou polygone afin de produire des cartes à des échelles plus petites. La simplification permet de réduire l’utilisation de la mémoire, du disque, et de la bande passante.
La fonction st_simplify() de la bibliothèque sf permet de simplifier des objets vectoriels de types ligne ou polygone en réduisant le nombre de points que ceux-ci comprennent. Souvenez-vous qu’une ligne est constituée d’une succession de points et qu’un polygone est constitué d’un ensemble de lignes.
Cette fonction est basée sur l’algorithme de Douglas-Peucker. Décrire le fonctionnement de cet algorithme dépasse l’objectif de ce cours. Grosso modo, l’algorithme fait appel à un seuil de distance (le paramètre dTolerance) qu’il utilise pour transformer en ligne droite toute courbe qui dévie d’une ligne droite par une quantité moindre que ce seuil. Cette distance reflète en quelque sorte la résolution que nous souhaitons atteindre avec l’objet simplifié.
Le seuil de tolérance étant une distance, nous l’exprimons en mètres. Nous devons alors nous assurer que l’objet spatial à simplifier est dans un système de coordonnées métriques.
En guise d’exemple, simplifions le shapefile des régions administratives du Québec :
regions_nad <- st_transform(regions, crs = 32198)
regions_simple_10 <- st_simplify(regions_nad, dTolerance = 10000) #10000m
regions_simple_40 <- st_simplify(regions_nad, dTolerance = 40000) #40000mRemarquez que nous avons d’abord transformé l’objet spatial regions dans le système de coordonnées de référence NAD83, dont le EPSG correspond à 32198, puisque l’unité de ce système est le mètre.
La fonction st_combine()
La fonction st_combine() de la bibliothèque sf sert à combiner des géométries afin d’en former une seule. Cette opération peut être utile lorsque nous souhaitons considérer plusieurs géométries comme formant un même objet spatial.
Reading layer `regn_tours_s250k_20160125' from data source `D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module7\data\regions_touristiques\Shapefile\regn_tours_s250k_20160125.shp'
using driver `ESRI Shapefile'
Simple feature collection with 21 features and 4 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -79.77 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: WGS 84Considérons le shapefile GIM contenant deux géométries: un polygone délimitant la Gaspésie et un polygone délimitant les Îles-de-la-Madeleine.
GIMSimple feature collection with 2 features and 2 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -68.52 ymin: 46.84 xmax: -60.4 ymax: 49.72
Geodetic CRS: WGS 84
Id Nom_reg
1 1 Îles-de-la-Madeleine
2 2 Gaspésie
geometry
1 MULTIPOLYGON (((-61 48.67, ...
2 MULTIPOLYGON (((-64.95 47.9...Maintenant, combinons ces deux polygones pour former une géométrie unique qui correspondra à la région administrative de la Gaspésie - Îles-de-la-Madeleine
GIM_combine <- st_combine(GIM)
GIM_combineGeometry set for 1 feature
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -68.52 ymin: 46.84 xmax: -60.4 ymax: 49.72
Geodetic CRS: WGS 84MULTIPOLYGON (((-61 48.67, -60.75 48.67, -60.5 ...Le nouvel objet GIM_combine est effectivement formé d’une seule géométrie. Notez cependant que la fonction st_combine() ne fusionne pas les frontières à l’intérieur du nouveau polygone formé. Pour unir deux polygones, il faut plutôt utiliser la fonction st_union() que nous définirons plus bas dans cette leçon.
La fonction st_cast()
La fonction st_cast() sert à convertir la géométrie d’un objet spatial donné vers une autre géométrie. Cette fonction comprend deux arguments : st_cast(x, to). Le premier argument, x, correspond à l’objet vectoriel dont on souhaite modifier la géométrie, alors que le second argument, to, correspond à la géométrie que l’on souhaite lui attribuer.
Donnons un exemple. Utilisons d’abord le shapefile regions pour isoler le polygone de la région administrative de la Mauricie grâce à la fonction subset() :
Mauricie <- subset(regions,Rgns_Ad=="Mauricie")
MauricieSimple feature collection with 1 feature and 1 field
Attribute-geometry relationship: aggregate (1)
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -75.52 ymin: 46.15 xmax: -71.89 ymax: 49
Geodetic CRS: GCS_Geographic_Coordinate_System
Rgns_Ad geometry
12 Mauricie POLYGON ((-74.47 48.95, -74...Nous observons que l’objet Mauricie est bel et bien de type polygone. Maintenant utilisons la fonction st_cast() pour transformer la géométrie de cet objet en type multiligne et multipoint :
Mauricie_lines <- st_cast(Mauricie, to = "MULTILINESTRING")
Mauricie_linesSimple feature collection with 1 feature and 1 field
Attribute-geometry relationship: aggregate (1)
Geometry type: MULTILINESTRING
Dimension: XY
Bounding box: xmin: -75.52 ymin: 46.15 xmax: -71.89 ymax: 49
Geodetic CRS: GCS_Geographic_Coordinate_System
Rgns_Ad geometry
12 Mauricie MULTILINESTRING ((-74.47 48...Mauricie_pts<-st_cast(Mauricie, to = "MULTIPOINT")
Mauricie_ptsSimple feature collection with 1 feature and 1 field
Attribute-geometry relationship: aggregate (1)
Geometry type: MULTIPOINT
Dimension: XY
Bounding box: xmin: -75.52 ymin: 46.15 xmax: -71.89 ymax: 49
Geodetic CRS: GCS_Geographic_Coordinate_System
Rgns_Ad geometry
12 Mauricie MULTIPOINT ((-74.47 48.95),...Nous observons que les deux nouveaux objets vectoriels ont bel et bien la géométrie souhaitée .
Dans cet exemple, nous avons en quelque sorte “décomposé” la géométrie d’un polygone en lignes puis en points. Or, la fonction st_cast() peut également servir à “consolider” des géométries.
En guise d’exemple, considérons l’objet villes_NQ_combo créé en isolant du shapefile villes_reg les villes situées dans la région administrative du Nord-du-Québec et en les combinant par l’utilisation de la fonction st_combine() :
villes_NQ <- subset(villes_reg, Rgns_Ad == "Nord-du-Québec")
villes_NQ_combo <- st_combine(villes_NQ)
villes_NQ_comboGeometry set for 1 feature
Geometry type: MULTIPOINT
Dimension: XY
Bounding box: xmin: -79.29 ymin: 49.05 xmax: -65.95 ymax: 62.42
Geodetic CRS: Geographic Coordinate SystemMULTIPOINT ((-76.25 51.69), (-78.75 51.49), (-7...Cet objet possède une géométrie multipoint où chaque point correspond à une municipalité du Nord-du-Québec.
Utilisons maintenant la fonction st_cast() pour transformer la géométrie de cet objet en ligne et en polygone :
villes_NQ_lines<-st_cast(villes_NQ_combo, to = "LINESTRING")
villes_NQ_linesGeometry set for 1 feature
Geometry type: LINESTRING
Dimension: XY
Bounding box: xmin: -79.29 ymin: 49.05 xmax: -65.95 ymax: 62.42
Geodetic CRS: Geographic Coordinate SystemLINESTRING (-76.25 51.69, -78.75 51.49, -73.87 ...villes_NQ_pol<-st_cast(villes_NQ_combo, to = "POLYGON")
villes_NQ_polGeometry set for 1 feature
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -79.29 ymin: 49.05 xmax: -65.95 ymax: 62.42
Geodetic CRS: Geographic Coordinate SystemPOLYGON ((-76.25 51.69, -78.75 51.49, -73.87 50...L’objet villes_NQ_lines correspond effectivement à un ensemble de lignes et l’objet villes_NQ_lines à un ensemble de polygones formés en reliant les points ensembles.
La fonction st_buffer()
Une zone tampon (appelée buffer en anglais) est un polygone dont les frontières sont définies par une distance donnée autour d’un objet vectoriel. Une zone tampon peut être créée autour de tout objet vectoriel, que ce soit des points, des lignes ou des polygones.
La création de zones tampons est généralement réalisée pour répondre à des questions de nature géographique. Par exemple, combien de garderies se situent à une distance de 2 km de ma maison ? Ou encore, combien de stations-service se situent à moins de 500 m de la route menant de Chelsey à Cantley en Outaouais ?
La fonction st_buffer() de la bibliothèque sf permet de créer des zones tampons. Cette fonction comprend obligatoirement deux arguments. Le premier correspond à l’objet vectoriel autour duquel nous souhaitons construire une zone tampon, et le deuxième argument définit la distance sur laquelle la zone tampon s’étendra autour de l’objet vectoriel. Comme pour la fonction st_simplify(), l’objet vectoriel auquel nous appliquons la fonction st_buffer() doit être exprimé dans un SCR d’unité de mesure métrique.
Construisons des zones tampons autour de la ville de La Pocatière, que nous avons isolée plus haut, en considérant deux distances différentes (7.1):
la_poc_nad <- st_transform(la_poc, crs = 32198)
la_poc_tampon10 <- st_buffer(la_poc_nad, dist = 10e3)
la_poc_tampon50 <- st_buffer(la_poc_nad, dist = 50e3)Notez que l’expression e3 correspond au chiffre 1000 (c’est-à-dire 10 exposent 3).
FIGURE 7.1: Deux zones tampons de 10 km (en bleu) et de 50 km (en vert) autour de la ville de La Pocatière
Maintenant, construisons des zones tampons autour des régions administratives de l’Abitibi-Témiscamingue et du Saguenay - Lac-Saint-Jean (7.2). Utilisons d’abord la fonction subset() pour isoler les polygones correspondants à ces régions à partir du shapefile regions_nad dont l’unité de mesure du SCR est le mètre.
# Isoler les polygones des deux régions
Abitibi <- subset(regions_nad, Rgns_Ad == "Abitibi-Témiscamingue")
SagStJean <- subset(regions_nad, Rgns_Ad == "Saguenay - Lac-Saint-Jean")
# Calculer une zone tampon pour chacun des polygones
Abitibi_tampon20 <- st_buffer(Abitibi, dist = 20e3) #20 km
SagStJean_tampon50 <- st_buffer(SagStJean, dist = 70e3) #70 kmFIGURE 7.2: Une zone tampon de 20 km autour de la région administrative de l’Abitibi-Témicamingue et une zone tampon de 70 km autour du Saguenay - Lac-Saint-Jean.
Notez que la zone tampon d’un polygone inclue le polygone d’origine. C’est-à-dire que ce n’est pas simplement une bordure autour du polygone.
La fonction st_centroid
Le centroïde d’un polygone en cartographie correspond approximativement au centre géométrique d’un polygone44. Ces coordonnées servent parfois à définir la localisation du polygone. La fonction st_centroid() de la bibliothèque sf permet de calculer le centroïde de polygones.
Déterminons le centroïde des polygones de l’Abitibi et du Saguenay - Lac-Saint-Jean (7.3). Notez que la fonction st_centroid() nécessite également que le polygone soit défini selon un SCR dont l’unité de mesure est le mètre.
centre_Abitibi <- st_centroid(Abitibi)
centre_AbitibiSimple feature collection with 1 feature and 1 field
Attribute-geometry relationship: aggregate (1)
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -689600 ymin: 483300 xmax: -689600 ymax: 483300
Projected CRS: NAD83 / Quebec Lambert
Rgns_Ad geometry
1 Abitibi-Témiscamingue POINT (-689572 483277)centre_SagStJean <- st_centroid(SagStJean)
centre_SagStJeanSimple feature collection with 1 feature and 1 field
Attribute-geometry relationship: aggregate (1)
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -233200 ymin: 645400 xmax: -233200 ymax: 645400
Projected CRS: NAD83 / Quebec Lambert
Rgns_Ad geometry
17 Saguenay - Lac-Saint-Jean POINT (-233243 645360)La fonction st_centroid() retourne un objet vectoriel de type point qui conserve les attributs du polygone.
FIGURE 7.3: Les centroïdes (en rouge) des régions de l’Abitibi-Témicamingue (en bleu) et du Saguenay - Lac-Saint-Jean (vert) calculés avec la fonction st_centroid().
La fonction st_coordinates
La fonction st_coordinates() permet de connaître les coordonnées d’un objet vectoriel. Trouvons, par exemple, les coordonnées de la ville de La Pocatière que nous avons isolée plus haut :
st_coordinates(la_poc) X Y
[1,] -70.04 47.37Dans le cas présent, les coordonnées sont exprimées en degrés. Le X correspond à la longitude et le Y, à la latitude. En effet, le SCR de la_poc utilise des longitudes-latitudes. Ceci peut-être confirmé en utilisant la fonction st_is_longlat() :
st_is_longlat(la_poc)[1] TRUED’autre part, l’objet la_poc_nad, que nous avons obtenu en transformant la_poc dans le SCR NAD83 utilise plutôt des mètres. Ainsi :
st_is_longlat(la_poc_nad)[1] FALSEConséquemment, les coordonnées identifiées par la fonction st_coordinates() sont en mètres :
st_coordinates(la_poc_nad) X Y
[1,] -116039 375793Notez que cette fonction peut être utilisée sur tout objet de type vectoriel (ligne, multiligne, polygone, etc.). La sortie correspondra alors à un tableau donnant les coordonnées de chaque point constituant l’objet.
Opérations topologiques entre deux couches
Les opérations topologiques décrivent les relations spatiales entre des objets45. Ces opérations sont équivalentes aux opérations ensemblistes en mathématiques, telles l’union ou l’intersection, mais s’appliquent cette fois à des objets définis par une géométrie.
La bibliothèque sf contient plusieurs opérateurs topologiques; par exemple: st_union(), st_intersection(), st_difference() et st_sym_difference(). Ces opérateurs forment un nouvel objet spatial à partir des deux objets spatiaux intérrogés. Par exemple, la géométrie de l’objet z formé par l’opération z <- st_union(x,y) est constituée de la géométrie de x et de celle de y sans toutefois qu’il y ait de chevauchement.
Pour illustrer les opérations topologiques entre deux objets vectoriels, considérons les polygones A et B créés en définissant des zones tampons à partir des polygones de l’Abitibi-Témiscamingue et du Saguenay - Lac-Saint-Jean respectivement.
A <- st_buffer(Abitibi, dist = 80e3)
B <- st_buffer(SagStJean, dist = 100e3)Calculons maintenant des opérations topologiques sur ces polygones :
union_AB <- st_union(A,B)
inter_AB <- st_intersection(A,B)
diff_AB <- st_difference(A,B)
diff_BA <- st_difference(B,A)
sym_diff_AB <- st_sym_difference(A,B)Observons les géométries produites par ces opérations :
Opérations topologiques de confirmation
Les opérations topologiques de confirmation sont des fonctions qui permettent de vérifier si deux objets spatiaux satisfont à une relation topologique donnée. Ces opérations ne créent pas un nouvel objet spatial, elles retournent plutôt une valeur binaire qui confirme si oui ou non la relation existe entre les deux objets interrogés.
La bibliothèque sf contient plusieurs opérateurs topologiques de confirmation; par exemple: st_intersects(), st_disjoint(), st_crosses(), st_overlaps(), st_touches(), st_within() et st_contains().
La fonction st_intersects
La fonction st_intersects() vérifie si deux objets spatiaux X et Y occupent un espace commun. La fonction confirmera qu’il y a bel et bien une intersection entre les deux objets si leurs intérieurs ou leurs frontières se recoupent. X et Y peuvent avoir n’importe quelle géométrie (point, multipoint, ligne, multiligne, polygone, multipolygone) (figure 7.4).
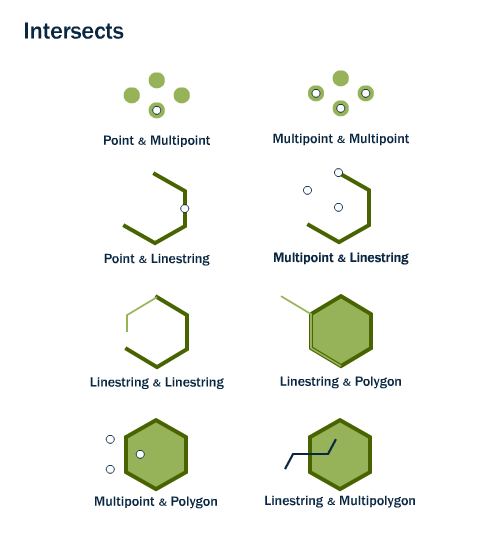
FIGURE 7.4: Combinaisons de géométries satisfaisant à la condition d’intersection. Récupérer sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Pour bien comprendre comment opère st_intersects() considérons le polygone A utilisé précédemment ainsi que l’objet spatial points constitué de cinq points de couleur différente.
pointsSimple feature collection with 5 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -902900 ymin: 476800 xmax: -224400 ymax: 668000
Projected CRS: NAD83 / Quebec Lambert
geometry couleur
1 POINT (-685765 476835) Bleu
2 POINT (-224449 667962) Rouge
3 POINT (-480113 560159) Violet
4 POINT (-395847 597020) Jaune
5 POINT (-902947 480553) Vert
FIGURE 7.5: Exemples illustrant la fonction st_intersects().
Utilisons a fonction st_intersects() pour déterminer quels points intersectent le polygone A :
st_intersects(points, A)Sparse geometry binary predicate list of length
5, where the predicate was `intersects'
1: 1
2: (empty)
3: 1
4: (empty)
5: 1
La sortie est exprimée sous forme d’une liste contenant 5 paires d’éléments; une paire pour chacun des points interrogés. Le premier élément d’une paire (c’est-dire,le chiffre avant le deux-points) correspond à l’indice du point. Le second élément prend la valeur 1 si le point intersecte le polygone A, et la valeur empty si le point ne recoupe pas le polygone A.
Il est aussi possible d’ajouter l’argument sparse = FALSE afin que la sortie s’exprime sous une forme matricielle d’éléments logiques.
st_intersects(points, A, sparse = FALSE) [,1]
[1,] TRUE
[2,] FALSE
[3,] TRUE
[4,] FALSE
[5,] TRUELa forme logique est particulièrement utile lorsque nous voulons filtrer les géométries qui satisfont à la condition d’intersection. Par exemple, cette commande retourne seulement les points qui intersectent le polygone A :
points[st_intersects(points, A, sparse = FALSE),]Simple feature collection with 3 features and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -902900 ymin: 476800 xmax: -480100 ymax: 560200
Projected CRS: NAD83 / Quebec Lambert
geometry couleur
1 POINT (-685765 476835) Bleu
3 POINT (-480113 560159) Violet
5 POINT (-902947 480553) VertQue se passent-ils si nous inversons les arguments de la fonction st_intersects() ?
st_intersects(A, points)Sparse geometry binary predicate list of length
1, where the predicate was `intersects'
1: 1, 3, 5Dans ce cas, la fonction retourne une liste d’une seule combinaison d’éléments associée au polygone interrogé. Cette fois, les éléments à droite du deux-points correspondent aux indices des points qui satisfont à la condition d’intersection.
La fonction st_disjoint
La fonction st_disjoint() vérifie la condition inverse de la fonction st_intersects(), c’est-à-dire l’absence d’intersection entre deux objets X et Y (figure 7.6).
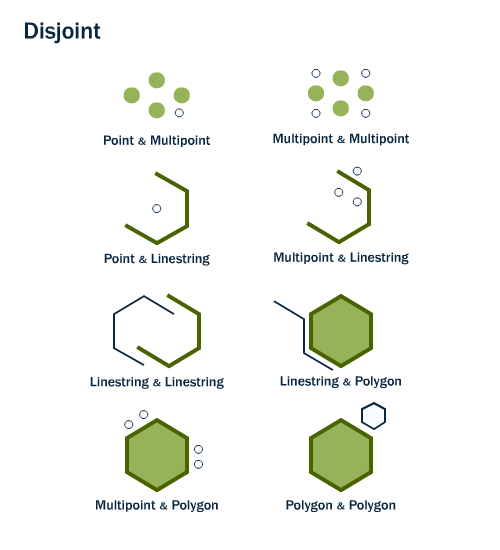
FIGURE 7.6: Combinaisons de géométries disjointes. Image récupérée sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Par exemple, la fonction st_disjoint() permet de confirmer que les points jaune et rouge sont disjoints du polygone A (Figure 7.5) :
st_disjoint(A, points)Sparse geometry binary predicate list of length
1, where the predicate was `disjoint'
1: 2, 4# ou encore
points$couleur[st_disjoint(A, points,sparse = FALSE)][1] "Rouge" "Jaune"
####### La fonction st_crosses {-}
La fonction st_crosses() vérifie si deux objets spatiaux X et Y se croisent. Cette fonction est donc similaire à la fonction st_intersects() mais elle contient des conditions supplémentaires:
- l’intersection entre les deux géométries inclue une partie mais pas l’entièreté de leurs intérieurs,
- la dimension géométrique de l’intersection doit être inférieure à la dimension maximale des deux géométries,
- l’intersection ne peut être égale à l’une ou l’autre des géométries.
La figure 7.7 illustre différentes combinaisons de géométries qui satisfont à la condition st_crosses.
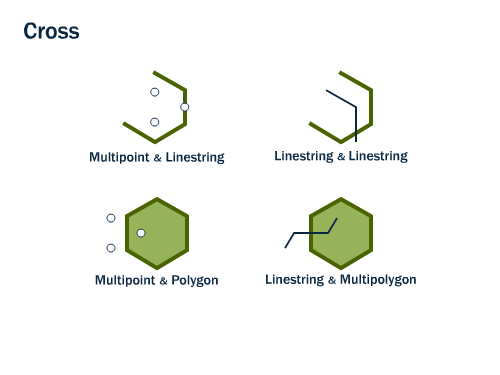
FIGURE 7.7: Combinaisons de géométries qui se croisent. Image récupérée sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Donnons quelques exemples pour démontrer en quoi la fonction st_crosses() diffère de la fonction st_intersects(). Pour ce faire, considérons les géométries illustrées à la figure 7.8.
FIGURE 7.8: Exemples illustrant la fonction st_crosses().
Bien que toutes ces géométries s’intersectent, elles ne se croisent pas toutes. Vérifions d’abord la condition d’intersection :
st_intersects(A,trait_bleu)Sparse geometry binary predicate list of length
1, where the predicate was `intersects'
1: 1st_intersects(A,trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `intersects'
1: 1st_intersects(A,B)Sparse geometry binary predicate list of length
1, where the predicate was `intersects'
1: 1Puis, la condition de croisement :
st_crosses(A,trait_bleu)Sparse geometry binary predicate list of length
1, where the predicate was `crosses'
1: (empty)st_crosses(A,trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `crosses'
1: 1st_crosses(A,B)Sparse geometry binary predicate list of length
1, where the predicate was `crosses'
1: (empty)Le trait bleu ne croise pas le polygone A car l’intersection entre ces deux géométries est égale au trait bleu. De plus, les polygones A et B ne se croisent pas non plus car leur intersection forme un polygone. Un polygone a une dimension géométrique de 2, tout comme les polygones A et B. Ainsi, seul le trait mauve croise le polygone A. En effet, une partie seulement de sa géométrie intersecte le polygone A, le reste étant situé à l’extérieur du polygone.
La fonction st_overlaps
La fonction st_overlaps() vérifie si l’intersection entre deux géométries de même dimension possède aussi la même dimension. De plus, cette intersection ne peut être égale à une des deux géométries interrogées. La figure 7.9 illustre différentes combinaisons de géométries qui satisfont à la condition de superposition.
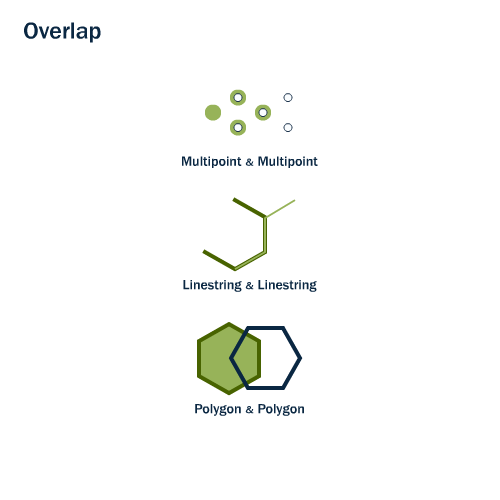
FIGURE 7.9: Combinaisons de géométries qui se superposent. Image récupérée sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Considérons les polygones A, B, ainsi que celui de l’Abitibi-Témiscamingue illustrés à la figure 7.10.
FIGURE 7.10: Exemples illustrant la fonction st_overlaps().
Les polygones A et B satisfont la condition de superposition car leur intersection est aussi un polygone. Par ailleurs, le polygone A et celui de l’Abitibi ne satisfont pas à la condition de superposition car l’intersection est identique au polygone de l’Abitibi-Témiscamingue.
st_overlaps(A,B)Sparse geometry binary predicate list of length
1, where the predicate was `overlaps'
1: 1st_overlaps(Abitibi,A)Sparse geometry binary predicate list of length
1, where the predicate was `overlaps'
1: (empty)
####### La fonction st_touches {-}
La fonction st_touches() vérifie si deux objets X et Y ont au moins un point en commun sans toutefois que leurs intérieurs s’intersectent. La figure 7.11 illustre différentes combinaisons de géométries qui se touchent.
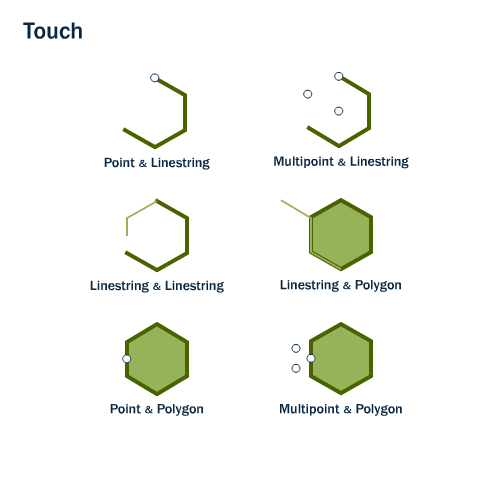
FIGURE 7.11: Combinaisons de géométries qui se touchent. Image récupérée sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Considérons par exemple les objets spatiaux illustrés à la figure :
La fonction st_touches() nous permet de vérifier que le polygone B, en rouge, touche au trait mauve et que le polygone A, en bleu, touche au point vert. Par ailleurs, la fonction confirme aussi que le polygone A ne touche pas au point bleu car ce sont leurs intérieurs qui s’intersectent. La même situation s’observe pour les polygones A et B qui partagent plus que leurs frontières. Cependant, les polygones de l’Abitibi-Témiscamingue, en vert, et de la Mauricie, en jaune, s’intersectent seulement le long de leurs frontières et ainsi se touchent.
st_touches(B, trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `touches'
1: 1st_touches(A, point_vert)Sparse geometry binary predicate list of length
1, where the predicate was `touches'
1: 1st_touches(A, point_bleu)Sparse geometry binary predicate list of length
1, where the predicate was `touches'
1: (empty)st_touches(A,B)Sparse geometry binary predicate list of length
1, where the predicate was `touches'
1: (empty)st_touches(Abitibi,Mauricie)Sparse geometry binary predicate list of length
1, where the predicate was `touches'
1: 1Les fonctions st_within et st_contains
La fonction st_within(X,Y) vérifie si l’objet X est entièrement à l’intérieur de l’objet Y. À l’opposé, la fonction st_contains(X,Y) vérifie si l’objet X contient entièrement l’objet Y. L’ordre des arguments est donc important dans l’utilisation de ces deux fonctions.
La figure 7.12 illustre différentes combinaisons de géométries qui sont contenues dans une autre géométrie.
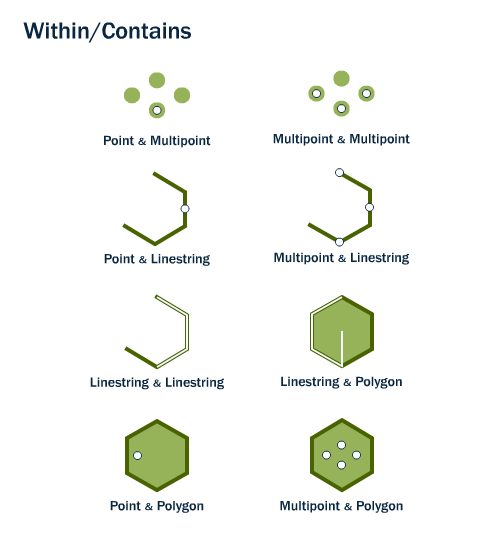
FIGURE 7.12: Combinaisons de géométries qui contiennent ou sont contenues dans une autre géométrie. Image récupérée sur le site de documentation de postgis: http://postgis.net/workshops/postgis-intro/spatial_relationships.html
Pour illustrer ces fonctions, considérons les objets spatiaux illustrés à la figure 7.13 :
FIGURE 7.13: Exemples illustrant les fonctions st_contains() et st_within().
La fonction st_contains() nous permet de vérifier que le polygone A, en bleu, contient le point bleu et le trait bleu. Par contre, le polygone A ne contient pas le trait mauve puisque ce dernier n’est pas entièrement à l’intérieur de A. De plus, le contour rose du polygone B contient entièrement le trait mauve.
st_contains(A, point_bleu)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: 1st_contains(A, trait_bleu)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: 1st_contains(A, trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: (empty)st_contains(contour_rose, trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: 1La fonction st_contains() comporte une subtilité qui peut être trompeuse. La condition st_contains(X,Y) est satisfaite, c’est-à-dire, l’objet X contient l’objet Y, si et seulement si aucun point de Y ne se trouve à l’extérieur de X, et qu’au moins un point de Y se trouve à l’intérieur de X46. En particulier, ceci signifie qu’un polygone ne contient jamais sa frontière. Ainsi, dans l’illustration de la figure 7.13, le polygone B, en rouge, ne contient pas le contour rose. Le polygone B ne contient pas non plus le trait mauve. Cependant, il contient le trait vert car ce dernier comporte des points à l’intérieur du polygone B.
st_contains(B, contour_rose)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: (empty)st_contains(B, trait_mauve)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: (empty)st_contains(B, trait_vert)Sparse geometry binary predicate list of length
1, where the predicate was `contains'
1: 1La fonction st_contains() vérifie exactement la condition inverse de la fonction st_within() :
st_within(point_bleu, A)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: 1st_within(trait_bleu, A)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: 1st_within(trait_mauve, A)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: (empty)st_within(trait_mauve, contour_rose)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: 1st_within(contour_rose, B)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: (empty)st_within(trait_mauve, B)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: (empty)st_within(trait_vert, B)Sparse geometry binary predicate list of length
1, where the predicate was `within'
1: 1La fonction st_join(), vue plus, qui permet de faire une jointure spatiale entre deux objets vectoriels s’appuie, par défaut, sur la fonction de confirmation st_intersects(). En effet, la fonction st_join(x,y) identifie la présence d’une intersection entre les éléments de x et de y puis assigne les attributs de y aux éléments de x qui satisfont cette condition d’intersection. Par ailleurs, il est possible d’utiliser la fonction st_join() en utilisant d’autres opérations topologiques de confirmation que celle par défaut. En effet, il est possible de définir un troisième argument, join, pour préciser une autre opération comme st_contains, st_touches, st_overlaps etc.
Donnons un exemple. Pour chaque région administrative du Québec, déterminons les régions qui lui sont adjacentes. Il s’agit ici d’utiliser la fonction st_join() avec la condition st_touches :
st_join(regions, regions, join = st_touches)Simple feature collection with 76 features and 2 fields
Geometry type: GEOMETRY
Dimension: XY
Bounding box: xmin: -79.76 ymin: 44.99 xmax: -56.93 ymax: 62.58
Geodetic CRS: GCS_Geographic_Coordinate_System
First 10 features:
Rgns_Ad.x
1 Abitibi-Témiscamingue
1.1 Abitibi-Témiscamingue
1.2 Abitibi-Témiscamingue
2 Bas-Saint-Laurent
2.1 Bas-Saint-Laurent
2.2 Bas-Saint-Laurent
2.3 Bas-Saint-Laurent
3 Capitale-Nationale
3.1 Capitale-Nationale
3.2 Capitale-Nationale
Rgns_Ad.y
1 Mauricie
1.1 Nord-du-Québec
1.2 Outaouais
2 Capitale-Nationale
2.1 Chaudière-Appalaches
2.2 Côte-Nord
2.3 Gaspésie - Îles-de-la-Madeleine
3 Bas-Saint-Laurent
3.1 Centre-du-Québec
3.2 Chaudière-Appalaches
geometry
1 POLYGON ((-75.52 47.85, -75...
1.1 POLYGON ((-75.52 47.85, -75...
1.2 POLYGON ((-75.52 47.85, -75...
2 POLYGON ((-67.15 49.19, -66...
2.1 POLYGON ((-67.15 49.19, -66...
2.2 POLYGON ((-67.15 49.19, -66...
2.3 POLYGON ((-67.15 49.19, -66...
3 POLYGON ((-72.07 47.95, -72...
3.1 POLYGON ((-72.07 47.95, -72...
3.2 POLYGON ((-72.07 47.95, -72...Cette fonction nous retourne un objet spatial composé de deux attributs. L’attribut de gauche, Rgns_Ad.x donne le nom de chaque polygone des régions administratives de regions alors que l’attribut de droite, Rgns_Ad.y, assigne à chacun de ces polygones, le nom d’une des régions administratives qui lui est voisine. Puisque chaque polygone possède plus d’une région voisine, leur nom et leur géométrie sont répétés pour chaque région voisine.
Opérations de mesure
Plusieurs fonctions de la bibliothèque sf permettent de calculer des mesures spatiales comme la distance, la superficie, ou la longueur.
La fonction st_distance()
La fonction st_distance() retourne la distance euclidienne entre deux objets spatiaux. Par exemple, nous pouvons utiliser cette fonction pour calculer la distance entre deux points. Calculons la distance qui sépare la ville de La Pocatière, dont nous avons isolé les coordonnées plus haut, et la ville de Rimouski.
# Isoler le point correspondant aux coordonnées de la ville
# de Rimouski à partir du shapefile des villes du Québec
rimouski <- subset(villes, toponyme == "Rimouski")
# Transformer rimouski dans le même SCR d'unité métrique que la_poc
rimouski_nad <- st_transform(rimouski, crs = 32198)
# Calculer la distance
distance_lapoc_rimou <- st_distance(la_poc_nad, rimouski_nad)
distance_lapoc_rimouUnits: [m]
[,1]
[1,] 164694La distance calculée est de 164693 m, soit environ as.integer(round(distance_lapoc_rimou[1]/1000)) km. Notez que nous avons calculé la distance géométrique et non la distance que l’odomètre d’une voiture calculerait en voyageant sur l’autoroute entre La Pocatière et Rimouski.
Observez que la fonction st_distance() retourne aussi l’unité de mesure, ici des mètres. En effet, l’objet retourné par cette fonction est de classe units :
class(distance_lapoc_rimou)[1] "units"Nous pouvons également utiliser la fonction st_distance() pour calculer la distance entre plusieurs points. Par exemple, considérons le shapefile villes et calculons la distance qui sépare La Pocatière de chacune des villes du Québec.
# Transformer le SRC de villes
villes_nad <- st_transform(villes, crs = 32198)
# Calculer les distances
distance_la_poc_villes <- st_distance(villes_nad, la_poc_nad)
# Assigner le nom des villes
rownames(distance_la_poc_villes) <- villes$toponyme
colnames(distance_la_poc_villes) <- "La Pocatière"
# Les premières entrées
head(distance_la_poc_villes)Units: [m]
La Pocatière
Blanc-Sablon 1032719
Lourdes-de-Blanc-Sablon 1027494
Nemiscau 654358
Waskaganish 775654
Saint-Augustin 926883
Chevery 833225Ou encore, calculons la distance qui sépare chacune des villes du Québec :
distance_villes_villes <- st_distance(villes_nad, villes_nad)
colnames(distance_villes_villes) <- villes$toponyme
rownames(distance_villes_villes) <- villes$toponyme
quelques_villes <- c(49, 154, 314, 549, 639)
distance_villes_villes[quelques_villes, quelques_villes]Units: [m]
Rouyn-Noranda Québec Gatineau Gaspé
Rouyn-Noranda 0 607593 399903 1069375
Québec 607593 0 373067 549266
Gatineau 399903 373067 0 921441
Gaspé 1069375 549266 921441 0
Montréal 514725 231996 163439 778264
Montréal
Rouyn-Noranda 514725
Québec 231996
Gatineau 163439
Gaspé 778264
Montréal 0Cette fois, la fonction st_distance() retourne une matrice pour laquelle chaque entrée correspond à la distance entre deux villes. Cette matrice est bien sûr symétrique et sa diagonale est nulle.
Nous pouvons aussi utiliser la fonction st_distance()pour calculer la distance entre un point et un polygone. Par exemple, calculons la distance entre le point correspondant au centre du polygone de l’Abitibi-Témiscamingue et le polygone du Saguenay - Lac-Saint-Jean (voir la figure 7.3).
st_distance(centre_Abitibi, SagStJean)Units: [m]
[,1]
[1,] 268327Notez que pour calculer la distance entre un polygone et un point, ce dernier doit être situé à l’extérieur du polygone, sans quoi cette fonction retourne la valeur zéro :
st_distance(centre_Abitibi, Abitibi)Units: [m]
[,1]
[1,] 0La distance entre deux polygones se calcule de façon similaire.
st_distance(Abitibi, SagStJean, by_element = TRUE)76459 [m]Cette mesure correspond à la plus petite distance séparant les deux polygones.
La fonction st_area()
La fonction st_area() calcule la superficie d’un polygone. Calculons par exemple la superficie des polygones illustrés à la figure 7.13) :
st_area(A)1.74e+11 [m^2]st_area(B)2.863e+11 [m^2]st_area(inter_AB)1.642e+10 [m^2]Remarquez que les unités, ici des mètres carrés, sont fournies. L’objet retourné par la fonction st_area() est aussi de classe units :
class(st_area(A))[1] "units"La superficie d’objets spatiaux de dimension inférieure à deux est bien nulle :
st_area(point_bleu)0 [m^2]st_area(trait_bleu)0 [m^2]La fonction st_length()
La fonction st_length() calcule la longueur d’un objet spatial unidimensionnel (LINESTRING, MULTILINESTRING).
st_length(trait_bleu)227718 [m]st_length(trait_mauve)361759 [m]st_length(contour_rose)2095138 [m]Comme pour les fonctions st_distance() et st_area(), la fonction st_length() retourne un objet de classe units.
La fonction calcule une longueur nulle pour les polygones ou les points :
st_length(A)0 [m]st_length(point_bleu)0 [m]La fonction set_units
Il peut être pratique de changer les unités de mesure avec lesquelles nous travaillons. Par exemple, utiliser les mètres carrés lorsque nous traitons de larges étendues peut être encombrant. La fonction set_units de la bibliothèque units permet de transformer les unités de mesure d’un objet ou d’en assigner à un objet sans unités.
Par exemple, pour les unités de longueur :
library(units)udunits database from C:/Users/efilotas/AppData/Local/R/win-library/4.3/units/share/udunits/udunits2.xmlL_m <- st_length(trait_bleu)
L_km <- set_units(L_m,km)
L_miles <- set_units(L_m, miles)
L_m227718 [m]L_km227.7 [km]L_miles141.5 [miles]Et, pour les unités d’aire :
A_m2 <- st_area(A)
A_km2 <- set_units(A_m2, km2)
A_ha <- set_units(A_m2, ha) # 1 hectare (ha) mesure 100 m x 100 m
A_m21.74e+11 [m^2]A_km2174004 [km2]A_ha17400384 [ha]7.1.3 Problématique à résoudre
Maintenant que nous avons appris les opérations de base pour manipuler les données vectorielles, nous sommes en mesure de résoudre la problématique énoncée au début de cette leçon :
Parmi les dix plus grandes villes du Québec, quelle est celle qui dispose du plus grand nombre de parcs nationaux dans un rayon de 70 km ?
Les étapes de la démarche de résolution sont les suivantes:
- Obtenir la taille de la population de chacune des municipalités.
- Filtrer ces municipalités pour retenir les 10 municipalités ayant la taille de population la plus importante.
- Lire la géodatabase du réseau de la SÉPAQ.
- Tracer une zone tampon de 70 km de rayon autour de chacune des dix plus grandes villes.
- Pour chaque zone, compter le nombre de parcs présent dans la zone tampon de 70 km.
- Déterminer la ville qui compte le plus grand nombre de parcs dans la zone tampon qui lui est associée.
Commençons!
1. Taille des populations pour chaque municipalité
Nous devons obtenir la taille de la population de chacune des municipalités québécoises. Nous avons déjà réalisé cette opération lorsque nous avons appris à utiliser la fonction merge().
En effet, nous avons associé à chaque municipalité contenue dans le shapefile villes la taille de sa population telle que donnée dans le dataframe pop. Nous avons utilisé la fonction merge() sur les colonnes toponyme et munnom qui agissent comme dénominateur commun des deux jeux de données. Voici un rappel de l’opération exécutée :
villes_pop <- merge(x = villes, y = pop, by.x="toponyme", by.y="munnom")
names(villes_pop)[2:3] <- c("superficie", "population") # Nous avions aussi changer le nom des colonnes!
head(villes_pop)Simple feature collection with 6 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -78.2 ymin: 45.65 xmax: -62.08 ymax: 60.81
Geodetic CRS: Geographic Coordinate System
toponyme superficie population
1 Acton Vale 91.1 7733
2 Aguanish 680.6 238
3 Akulivik 82.3 678
4 Albanel 205.0 2232
5 Alma 232.6 30831
6 Amherst 249.5 1459
geometry
1 POINT (-72.56 45.65)
2 POINT (-62.08 50.22)
3 POINT (-78.2 60.81)
4 POINT (-72.44 48.88)
5 POINT (-71.65 48.54)
6 POINT (-64.21 45.83)2. Dix municipalités les plus grandes
Nous devons filtrer l’objet villes_pop et sélectionner les 10 municipalités de plus grande population. Tout d’abord, il s’agit d’ordonner l’attribut population contenu dans l’objet villes_pop. Pour ce faire, nous allons utiliser la fonction order():
villes_pop <- villes_pop[order(villes_pop$population, decreasing = TRUE), ]L’objet villes_pop est maintenant ordonné de manière décroissante en fonction de la taille de la population des municipalités. Ainsi, les 10 premières lignes de cet objet correspondent aux 10 municipalités les plus grandes du Québec. On peut donc assigner les 10 premières lignes à un nouvel objet intitulé top10_villes:
top10_villes <- villes_pop[1:10, ]
top10_villesSimple feature collection with 10 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -75.64 ymin: 45.31 xmax: -71.18 ymax: 46.81
Geodetic CRS: Geographic Coordinate System
toponyme superficie population
204 Montréal 431.7 1801546
240 Québec 485.2 546958
166 Laval 266.8 439754
94 Gatineau 380.6 286755
175 Longueuil 122.6 249338
442 Sherbrooke 366.0 169136
174 Lévis 498.3 147440
456 Trois-Rivières 334.2 138134
449 Terrebonne 158.5 117664
336 Saint-Jean-sur-Richelieu 233.7 98036
geometry
204 POINT (-73.56 45.51)
240 POINT (-71.21 46.81)
166 POINT (-73.75 45.55)
94 POINT (-75.64 45.48)
175 POINT (-73.52 45.54)
442 POINT (-71.89 45.4)
174 POINT (-71.18 46.8)
456 POINT (-72.54 46.34)
449 POINT (-73.63 45.69)
336 POINT (-73.25 45.31)Visualisons ce nouvel objet avec la fonction mapview().
mapview(top10_villes, zcol= "population")3. Géodatabase du réseau de la SÉPAQ
La troisième étape consiste à charger la couche d’informations spatiales contenant les différentes aires récréatives du Québec. Cette information se trouve à l’intérieur de la géodatabase parcs.gdb disponible dans le répertoire Module7_donnees que vous avez téléchargé au début de la leçon.
Comme vu dans le module 4, les géodatabase permettent de contenir plusieurs couches vectorielles. Nous devons donc lire la géodatabase et explorer les différentes couches afin de déterminer celle qui correspond aux aires récréatives.
st_layers("Module7/Module7_donnees/parcs.gdb") Driver: OpenFileGDB
Available layers:
layer_name geometry_type features fields crs_name
1 Terafc_s Multi Polygon 5 18 NAD83
2 Terpnq_s Multi Polygon 27 18 NAD83
3 Terfer_s Multi Polygon 1 18 NAD83
4 Terpla_s Multi Polygon 27 18 NAD83
5 Terpma_s Multi Polygon 1 18 NAD83
6 Terpnc_s Multi Polygon 4 18 NAD83
7 Terrec_s Multi Polygon 72 18 NAD83
8 Terref_s Multi Polygon 21 18 NAD83
9 Terrfa_s Multi Polygon 9 18 NAD83
10 Terrnf_s Multi Polygon 8 18 NAD83
11 Terrom_s Multi Polygon 28 18 NAD83
12 Tersfo_s Multi Polygon 1 18 NAD83
13 Tertec_s Multi Polygon 1 18 NAD83
14 Terzec_s Multi Polygon 86 18 NAD83
15 Terepa_s Multi Polygon 1 18 NAD83
16 Terpde_s Multi Polygon 189 18 NAD83
17 Terpre_s Multi Polygon 17 18 NAD83Nous pouvons remarquer que les intitulés des différentes couches ne sont pas bien définis. Il faut donc prendre le temps de regarder la documentation accessible sur le site de données ouvertes Québec. Ne vous inquiétez pas, je l’ai fait pour vous! En nous intéressant à la structure de données et à la nomenclature utilisée et décrite, nous pouvons déterminer que la couche terpnq_s correspond aux territoires des parcs nationaux du Québec. Nous pouvons donc faire la lecture de la géodatabase avec la fonction st_read() en précisant cette couche à l’aide de l’argument layer.
parcs_nationaux <- st_read("Module7/Module7_donnees/parcs.gdb", layer = "terpnq_s") Reading layer `terpnq_s' from data source
`D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module7\Module7_donnees\parcs.gdb'
using driver `OpenFileGDB'
Simple feature collection with 27 features and 18 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -79.39 ymin: 45.29 xmax: -62.41 ymax: 61.45
Geodetic CRS: NAD83Visualisons les polygones de parcs_nationaux.
mapview(parcs_nationaux, zcol = "TRQ_NM_TER", legend = FALSE)Notez que l’attribut “TRQ_NM_TER” de l’objet parcs_nationaux correspond au nom de chaque parc national.
parcs_nationaux$TRQ_NM_TER [1] "Parc national des Pingualuit"
[2] "Parc national Kuururjuaq"
[3] "Parc national Ulittaniujalik"
[4] "Parc national Tursujuq"
[5] "Parc national d'Anticosti"
[6] "Parc national de la Gaspésie"
[7] "Parc national de la Pointe-Taillon"
[8] "Parc national des Monts-Valin"
[9] "Parc national d'Aiguebelle"
[10] "Parc national de l'Île-Bonaventure-et-du-Rocher-Percé"
[11] "Parc national du Fjord-du-Saguenay"
[12] "Parc national du Bic"
[13] "Parc national de Miguasha"
[14] "Parc national des Hautes-Gorges-de-la-Rivière-Malbaie"
[15] "Parc national du Lac-Témiscouata"
[16] "Parc national des Grands-Jardins"
[17] "Parc national de la Jacques-Cartier"
[18] "Parc national d'Opémican"
[19] "Parc national du Mont-Tremblant"
[20] "Parc national de Frontenac"
[21] "Parc national des Îles-de-Boucherville"
[22] "Parc national de Plaisance"
[23] "Parc national du Mont-Saint-Bruno"
[24] "Parc national d'Oka"
[25] "Parc national du Mont-Mégantic"
[26] "Parc national de la Yamaska"
[27] "Parc national du Mont-Orford" 4. Zones tampons autour des plus grandes municipalités
Nous traçons maintenant une zone tampon (POLYGON) de 70 km de rayon autour de chaque municipalité (POINT) du shapefile top10_villes. Pour ce faire, nous allons utiliser la fonction st_buffer(). Avant de réaliser cette opération, nous devons vérifier que le système de coordonnées de référence de l’objet spatial top10_villes est défini en unité métrique. En effet, la distance de 70 km pourrait être interprétée comme étant 70 degrés si l’unité de la projection était en degré. Attention, cette erreur est très courante! Lorsque l’on veut calculer des distances euclidiennes, il faut toujours s’assurer que l’unité du système de projection est en mètre et non en degré.
st_crs(top10_villes)$proj4string [1] "+proj=longlat +ellps=GRS80 +no_defs"+proj=longlat atteste que la projection est en degré. Nous allons donc reprojeter l’objet top10_villes dans le système de coordonnées de référence NAD83 qui est métrique et dont le EPSG est 32198. NAD83 correspond au système de coordonnées Conique conforme de Lambert.
top10_villes_lcc <- st_transform(top10_villes, crs = 32198)
# On valide que les unités sont métriques (+units=m)
st_crs(top10_villes_lcc)$proj4string [1] "+proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs"Traçons à présent les zones tampon (buffer) autour des municipalités à l’aide de la fonction st_buffer() comme expliqué précédemment, et visualisons le résultat de cette opération.
top10_villes_buffer <- st_buffer(top10_villes_lcc, dist = 70e3) # 70 kms en mètres = 70e3
mapview(top10_villes_buffer, zcol = "toponyme", legend = FALSE)Rappelons que le premier argument de la fonction st_buffer() correspond à l’objet spatial à partir duquel nous créons les zones tampons, et le second argument correspond à la longueur du rayon des zones tampons en mètres (70 km = 70e3 m).
5. Nombre de parcs dans chaque zone tampon
Nous allons utiliser la fonction st_intersects() pour déterminer quels parcs de l’objet parcs_nationaux se trouvent, partiellement ou entièrement, à l’intérieur de chacune des zones tampons de l’objet top10_villes_buffer. Avant de réaliser cette opération spatiale, nous devons nous assurer que les deux objets spatiaux (top10_villes_buffer et parcs_nationaux) utilisent le même système de coordonnées de référence.
st_crs(top10_villes_buffer) == st_crs(parcs_nationaux)[1] FALSEPuisque la réponse est négative, transformons le SCR de l’objet parcs_nationaux.
parcs_nationaux_lcc = st_transform(parcs_nationaux, crs = st_crs(top10_villes_buffer))Nous pouvons maintenant utiliser la fonction st_intersects():
st_intersects(x = top10_villes_buffer, y = parcs_nationaux_lcc, sparse = FALSE) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[2,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[3,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[4,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[5,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[6,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[7,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[8,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[9,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[10,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16]
[1,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[2,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[3,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[4,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[5,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[6,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[7,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[8,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[9,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[10,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
[1,] FALSE FALSE FALSE FALSE TRUE FALSE TRUE TRUE
[2,] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[3,] FALSE FALSE FALSE FALSE TRUE FALSE TRUE TRUE
[4,] FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE
[5,] FALSE FALSE FALSE FALSE TRUE FALSE TRUE TRUE
[6,] FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE
[7,] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[8,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[9,] FALSE FALSE FALSE FALSE TRUE FALSE TRUE TRUE
[10,] FALSE FALSE FALSE FALSE TRUE FALSE TRUE TRUE
[,25] [,26] [,27]
[1,] FALSE FALSE FALSE
[2,] FALSE FALSE FALSE
[3,] FALSE FALSE FALSE
[4,] FALSE FALSE FALSE
[5,] FALSE FALSE FALSE
[6,] TRUE TRUE TRUE
[7,] FALSE FALSE FALSE
[8,] FALSE FALSE FALSE
[9,] FALSE FALSE FALSE
[10,] FALSE TRUE FALSELa fonction st_intersects avec l’argument sparse = FALSE retourne une matrice avec en ligne les zones tampons des 10 plus grandes villes (argument x ci-dessus) et en colonne, les 27 parcs nationaux du Québec (argument y ci-dessus). Pour chacune des combinaisons, la valeur booléenne renvoyée (TRUE ou FALSE) spécifie si les deux polygones se chevauchent (partiellement ou non).
L’une des propriétés intéressantes des valeurs booléennes (TRUE ou FALSE), renvoyées par la fonction st_intersects, est que la valeur TRUE peut être interprétée par R comme une valeur de 1 et FALSE comme une valeur de 0. Il est donc possible de réaliser des opérations mathématiques sur des valeurs booléennes.
Par exemple, nous pouvons effectuer une sommation sur les lignes (zones tampons de chaque grande municipalité) afin de déterminer combien de parcs nationaux se trouvent à l’intérieur des zones tampons (c-à-d combien d’éléments ont la valeur TRUE).
rowSums(st_intersects(x = top10_villes_buffer, y = parcs_nationaux_lcc, sparse = FALSE)) [1] 3 1 3 1 3 4 1 0 3 4Consignons à présent ces valeurs dans une nouvelle colonne de la table d’attributs de l’objet top10_villes.
top10_villes$nbr_parcs <- rowSums(st_intersects(x = top10_villes_buffer, y = parcs_nationaux_lcc, sparse = FALSE))
top10_villesSimple feature collection with 10 features and 4 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -75.64 ymin: 45.31 xmax: -71.18 ymax: 46.81
Geodetic CRS: Geographic Coordinate System
toponyme superficie population
204 Montréal 431.7 1801546
240 Québec 485.2 546958
166 Laval 266.8 439754
94 Gatineau 380.6 286755
175 Longueuil 122.6 249338
442 Sherbrooke 366.0 169136
174 Lévis 498.3 147440
456 Trois-Rivières 334.2 138134
449 Terrebonne 158.5 117664
336 Saint-Jean-sur-Richelieu 233.7 98036
geometry nbr_parcs
204 POINT (-73.56 45.51) 3
240 POINT (-71.21 46.81) 1
166 POINT (-73.75 45.55) 3
94 POINT (-75.64 45.48) 1
175 POINT (-73.52 45.54) 3
442 POINT (-71.89 45.4) 4
174 POINT (-71.18 46.8) 1
456 POINT (-72.54 46.34) 0
449 POINT (-73.63 45.69) 3
336 POINT (-73.25 45.31) 46. Ville qui compte le plus grand nombre de parcs
Pour répondre à la question posée, ordonnons la table d’attributs de l’objet top10_villes en se basant sur la nouvelle colonne nbr_parcs.
top10_villes <- top10_villes[order(top10_villes$nbr_parcs, decreasing = TRUE), ]
top10_villesSimple feature collection with 10 features and 4 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -75.64 ymin: 45.31 xmax: -71.18 ymax: 46.81
Geodetic CRS: Geographic Coordinate System
toponyme superficie population
442 Sherbrooke 366.0 169136
336 Saint-Jean-sur-Richelieu 233.7 98036
204 Montréal 431.7 1801546
166 Laval 266.8 439754
175 Longueuil 122.6 249338
449 Terrebonne 158.5 117664
240 Québec 485.2 546958
94 Gatineau 380.6 286755
174 Lévis 498.3 147440
456 Trois-Rivières 334.2 138134
geometry nbr_parcs
442 POINT (-71.89 45.4) 4
336 POINT (-73.25 45.31) 4
204 POINT (-73.56 45.51) 3
166 POINT (-73.75 45.55) 3
175 POINT (-73.52 45.54) 3
449 POINT (-73.63 45.69) 3
240 POINT (-71.21 46.81) 1
94 POINT (-75.64 45.48) 1
174 POINT (-71.18 46.8) 1
456 POINT (-72.54 46.34) 0Nous constatons que Sherbrooke et Saint-Jean-sur-Richelieu disposent toutes deux du plus grand nombre (4) de parcs nationaux dans un rayon de 70 km!
Le centre géométrique d’une forme planaire est la moyenne des positions de tous les points constituants la forme. Vous pouvez trouver des informations supplémentaires sur le centroïde [ici]^(http://wiki.gis.com/wiki/index.php/Centroid).↩︎
https://geocompr.robinlovelace.net/spatial-operations.html#topological-relations↩︎
http://lin-ear-th-inking.blogspot.com/2007/06/subtleties-of-ogc-covers-spatial.html↩︎