8.1 Leçon
Au module 5, vous avez appris les fonctions essentielles pour lire et visualiser des données spatiales matricielles sous R. Le présent module vous amènera maintenant à manipuler conjointement des données matricielles et vectorielles.
Dans un premier temps, cette leçon vous enseignera le fonctionnement d’opérations de base sur les données matricielles.
Dans un second temps, cette leçon vous guidera dans la résolution d’une problématique qui nécessite de manipuler des données matricielles. Au cours des différentes étapes permettant de résoudre la problématique, vous mettrez en pratique les diverses fonctions R apprises jusqu’à maintenant. Plus précisément, nous allons pousser plus loin la problématique étudiée au module 7 en répondant aux deux questions suivantes:
Parmi les quatre parcs nationaux de la région de Sherbrooke, lequel dispose du plus haut sommet?
Quel est le profil topographique du sentier se rendant au plus proche de ce sommet?
8.1.1 Télécharger les données
Dans cette leçon, nous allons utiliser le modèle d’élévation numérique aussi appelé Digital Elevation Model (DEM). Cette couche d’information spatiale est produite par le gouvernement du Canada (accessible sur ce portail). Cette couche est une matrice de données (raster) contenant des valeurs d’élévation en mètres.
Nous allons également nous servir de la base de données vectorielles des sentiers de randonnées de la SÉPAQ (source), ainsi que celle des parcs nationaux de la région de Sherbrooke identifiés au module 7.
Afin de faciliter le téléchargement de ces données, l’ensemble de ces couches d’informations spatiales peuvent être téléchargée en cliquant sur un seul lien: données pour le module 8. Une fois téléchargé, le dossier compressé (zip) doit être dézippé dans votre répertoire de travail. Le dossier Module8_donnees comprend deux sous-dossiers et un fichier:
- parcs_sherbrooke
- DEM.tif
- sentiers_sepaq
8.1.2 Opération de bases
Dans cette section, nous allons nous familiariser avec les opérations fréquemment utilisées sur les données matricielles.
8.1.2.1 Importer et visualiser les données
Dans allons d’abord importer les différentes couches d’informations spatiales dans l’environnement R. Nous commençons par charger les bibliothèques requises pour importer les données spatiales vectorielles (sf), pour importer les données spatiales matricielles (raster) et pour visualiser ces données (mapview).
library(sf)
library(raster)
library(mapview)Ensuite, nous utilisons la fonction st_read() pour importer le shapefile parcs_sherbrooke qui contient les quatre parcs se situant dans un rayon de 70 km de la municipalité de Sherbrooke (voir la problématique du module 7).
parcs <- st_read("Module8/Module8_donnees/parcs_sherbrooke/parcs_sherbrooke.shp")Reading layer `parcs_sherbrooke' from data source
`D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module8\Module8_donnees\parcs_sherbrooke\parcs_sherbrooke.shp'
using driver `ESRI Shapefile'
Simple feature collection with 4 features and 18 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: -323500 ymin: 151800 xmax: -201900 ymax: 226200
Projected CRS: NAD83 / Quebec LambertEnfin, nous importons la couche d’élévation DEM pour la région d’intérêt en utilisant la fonction raster().
dem <- raster("Module8/Module8_donnees/DEM.tif")Nous visualisons ensuite les deux objets spatiaux afin de valider l’importation en utilisant la fonction mapview().
mapview(dem) + mapview(parcs, zcol = "TRQ_NM_")Notez que l’attribut TRQ_NM_ correspond aux noms des parcs nationaux.
8.1.2.2 Filtrer les cellules d’un raster
Une des opérations les plus fréquentes sur les raster est celle de filtrer les cellules (ou pixels). Ceci peut être fait dans le but de sélectionner des cellules possédant une valeur d’attribut particulière. Par exemple, à partir d’une couche matricielle des différentes classes d’utilisation du sol pour une région donnée, nous pourrions vouloir sélectionner les pixels de la classe “Eaux” ou encore ceux de la classe “Terres humides”.
Filtrer les cellules peut également être fait dans le but de sélectionner des cellules sur la base de leur localisation spatiale. Par exemple, nous pourrions vouloir choisir les cellules d’un raster qui sont à l’intérieur des limites administratives d’une municipalité.
Dans les sous-sections qui suivent, nous présenterons des fonctions qui permettent de réaliser ces deux types d’opération de filtrage de données matricielles.
Filtrer en utilisant la valeur des cellules
Fonction which()
Au module 5, nous avons vu comment accéder et manipuler les données de raster en utilisant, entre autres, les fonctions summary() et getValues(). Il est ainsi possible d’avoir une idée de la distribution des valeurs du raster dem en utilisant la ligne de commande suivante :
summary(getValues(dem)) Min. 1st Qu. Median Mean 3rd Qu. Max.
30 211 303 314 410 1174
NA's
3839 Nous pouvons apercevoir que certaines cellules du raster dem contiennent des valeurs négatives. Notez que ces valeurs ne sont pas aberrantes et signifient simplement que ces pixels se retrouvent en dessous du niveau de la mer. Pour la suite de la leçon (et à titre d’exemple), nous allons exclure ces valeurs négatives. En d’autres termes, nous allons appliquer un filtre sur les cellules du raster, filtre qui ne laissera passer que les valeurs positives.
Plus précisément, nous allons utiliser la fonction which() pour filtrer les données du raster dem. Rappelons que la fonction which() identifie la position des éléments de valeur TRUE dans un vecteur logique (voir le module 7 pour un rappel). Utilisons donc cette fonction pour trouver les cellules qui ont des valeurs d’élévation négatives.
ind <- which(getValues(dem) < 0)
indinteger(0)La ligne de commande ci-dessus retourne les indices des cellules qui satisfont la condition demandée (c’est-à-dire avoir une valeur négative).
Pour savoir combien de cellules possèdent une valeur d’élévation négative, nous pouvons tout simplement compter le nombre d’éléments contenus dans le vecteur retourné par la fonction which(). Si les cellules identifiées étaient nombreuses ou si nous avions besoin de conserver ce nombre en mémoire pour l’utiliser dans la suite de notre analyse, nous pourrions obtenir ce compte en utilisant la fonction générale length() qui retourne la taille d’un vecteur:
nombre <- length(ind)
nombre[1] 0Notons qu’il est aussi possible d’accéder aux valeurs de ces cellules en utilisant les indices ind identifiés:
getValues(dem)[ind]numeric(0)Nous observons que les valeurs sont belles et bien négatives!
Pour filtrer ces cellules aux valeurs négatives, c’est-à-dire exclure ces valeurs de notre analyse, nous allons remplacer leur valeur par le terme NA. Rappelons que NA signifie non applicable.
dem[ind] <- NAVoyons maintenant comment cette modification aux valeurs de certaines cellules altère les statistiques générales sur les valeurs du raster dem :
summary(getValues(dem)) Min. 1st Qu. Median Mean 3rd Qu. Max.
30 211 303 314 410 1174
NA's
3839 L’élévation minimale est maintenant de 2 et le nombre de NA a augmenté de 0. Ceci confirme que notre filtre a bien été appliqué.
La fonction which() peut aussi être utilisée pour filtrer des données selon des expressions logiques plus complexes. Nous pouvons, par exemple, remplacer getValues(dem) < 0 par getValues(dem) < 0 | getValues(dem) > 1000 pour exclure également les cellules avec des valeurs plus grandes que 1000 m. De plus, il est aussi possible de changer les valeurs des cellules identifiées en d’autres valeurs que NA.
Fonction reclassify
La fonction reclassify() de la bibliothèque raster permet également de filtrer des données matricielles et de leur assigner de nouvelles valeurs.
Démontrons son utilisation par un cas simple. Nous allons catégoriser le niveau d’élévation, c’est-à-dire les valeurs du raster dem, en trois catégories:
- catégorie 1: classe d’élévation faible allant de 0 à 250 m,
- catégorie 2: classe d’élévation modérée allant de 251 à 500 m,
- catégorie 3: classe d’élévation forte allant de 501 à 1200 m.
Avant de pouvoir utiliser la fonction reclassify(), il est nécessaire de construire une matrice indiquant les bornes limites des différentes classes.
nouvelles_classes <- matrix(c(0, 250, 1, 250, 500, 2, 500, 1200, 3), nrow = 3, ncol = 3, byrow = TRUE)
colnames(nouvelles_classes) <- c("Limite_min", "Limite_max", "nouvelles_classes")
nouvelles_classes Limite_min Limite_max nouvelles_classes
[1,] 0 250 1
[2,] 250 500 2
[3,] 500 1200 3Cette matrice est utilisée comme argument de la fonction reclassify() afin d’assigner les nouvelles classes aux valeurs du raster dem.
nouvelles_classes_dem <- reclassify(dem, nouvelles_classes, rigth = FALSE)Notez que l’utilisation par défaut de la fonction reclassify() inclue la borne supérieure mais pas la borne inférieure de l’intervalle de reclassification (]limite_lim, limite_max]). L’ajout de l’argument rigth = FALSE vient spécifier que nous souhaitons le contraire, c’est-à-dire l’inclusion de la borne inférieure mais pas de la borne supérieure ([limite_lim, limite_max[). Ainsi, nous avons précisé que les valeurs incluses dans la nouvelle classe 1 vont de 0 à 249 m plutôt que de 1 à 250 m.
Visualisons la nouvelle classification du domaine de valeurs du raster d’élévation dem à l’aide de la fonction mapview():
mapview(nouvelles_classes_dem)Notez que nous pouvons aussi utiliser NA pour exclure certaines cellules:
nouvelles_classes2 <- matrix(c(0, 250, NA, 250, 500, 2, 500, 1200, 3), nrow = 3, ncol = 3, byrow = TRUE)
mapview(reclassify(dem, nouvelles_classes2))Filtrer en utilisant les coordonnées spatiales des cellules
Une des opérations les plus fréquentes sur les raster est de filtrer les cellules en fonction de leurs coordonnées spatiales. Dans cette section, nous allons apprendre à utiliser les fonctions crop() et mask() pour réaliser ces manipulations.
Fonction crop()
La fonction crop() vous permet de rogner un raster, autrement dit d’utiliser un rectangle pour filtrer les cellules selon qu’elles soient ou non à l’intérieur de ce dernier.
Pour utiliser la fonction crop(), nous avons besoin de deux objets. Le premier objet est le raster à rogner et le second objet est le rectangle avec lequel le raster sera rogné. Ce rectangle est un objet de classe Extent (étendue en français). Un tel objet peut être créé en utilisant les coordonnées de ses coins inférieur-gauche (xmin, ymin) et supérieur-droit (xmax, ymax):
ext <- extent(c(-72, -71.5, 45.2, 45.8))
ext class : Extent
xmin : -72
xmax : -71.5
ymin : 45.2
ymax : 45.8 Avec la fonction plot(), nous pouvons visualiser la partie du raster qui sera rognée. Notez que la fonction mapview() ne peut pas être utilisée pour visualiser des objets de classe Extent.
plot(dem)
plot(ext, add = TRUE) 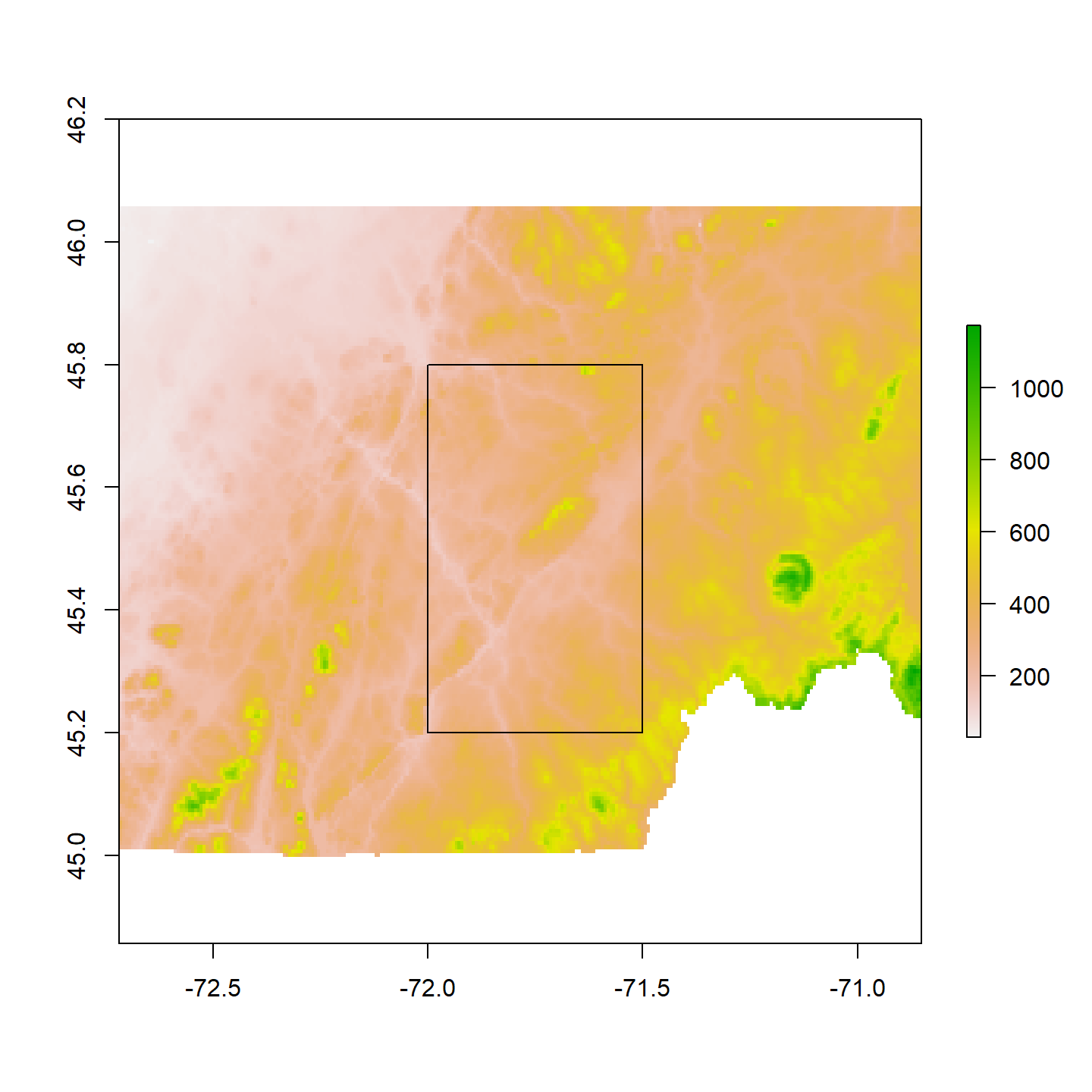
Il est très important de relever que de manière implicite les valeurs des coordonnées utilisées dans extent() sont exprimées dans le SCR de notre raster dem.
Utilisons maintenant la fonction crop() dont le premier argument est le raster à rogner et le second argument est l’objet de classe Extent.
dem_cr <- crop(dem, ext)La sortie est un raster (que nous appelons dem_cr) qui est recadré selon ext. Les cellules qui ne sont pas dans ce rectangle sont exclues.
mapview(dem_cr)La fonction crop() accepte en second argument, non seulement les objets de classe Extent, mais aussi tout objet à partir duquel un objet de classe Extent peut être extrait. Ceci signifie que le second argument peut aussi comprendre les objets spatiaux de classe RasterLayer et de classe sf.
En guise d’exemple, nous allons maintenant rogner le raster dem en utilisant les limites du premier parc de la SÉPAQ identifié dans les données vectorielles parcs. Il est en effet possible d’extraire un objet de classe Extent à partir de ces données. Vérifions-le en utilisant la fonction extent():
extent(parcs[1,])class : Extent
xmin : -215252
xmax : -201928
ymin : 195972
ymax : 226160 Avant d’utiliser la fonction crop() nous avons besoin de re-projeter le raster dem dans le SCR des données vectorielles parcs (notez que nous pourrions aussi faire l’inverse). L’opération qui suit utilise de façon implicite l’étendue spatiale de parcs[1, ] pour rogner dem_lcc.
dem_lcc <- projectRaster(dem, crs = crs(parcs))
dem_cr_p <- crop(dem_lcc, parcs[1, ])
mapview(dem_cr_p)Fonction mask()
La fonction mask() permet de découper un raster avec un polygone de n’importe quelle forme et non uniquement selon un rectangle. Pour illustrer cette fonction nous allons d’abord créer un polygone avec la fonction st_as_sf() de la bibliothèque sf (voir le module 4) :
# `mat` est une matrice 7x2 des coordonnées du polygone.
mat <- matrix(c( -72.5, 45.8,
-72, 45.5,
-72.5, 45.2,
-71.5, 45.4,
-71.7, 45.6,
-71.5, 45.7,
-72.5, 45.8), ncol = 2, byrow = TRUE)
# nous transformons mat en un data frame puis en un objet de class `sf`
pol <- st_as_sf(
data.frame(
var = 1,
geom = st_sfc(st_polygon(x = list(mat)))
),
crs = st_crs(dem)
)Notons que nous avons utilisé le même SCR que dem. Regardons ce à quoi ressemble le polygone que nous venons de créer.
mapview(dem)+mapview(pol)La fonction mask() permet de sélectionner uniquement les cellules du raster dem qui sont à l’intérieur du polygone pol (passé en second argument):
dem_ma <- mask(dem, pol)
mapview(dem_ma)La fonction mask() est dotée d’un argument inverse qui, s’il prend la valeur TRUE, permet de sélectionner toutes les cellules d’un raster qui sont à l’extérieur du polygone fourni:
dem_ma_inv <- mask(dem, pol, inverse = TRUE)
mapview(dem_ma_inv)La fonction mask() permet ainsi de filtrer les données matricielles de façon plus complexe qu’avec la fonction which(). En effet, les valeurs du raster dem_ma correspondent aux valeurs du sous-ensemble des cellules de dem qui sont à l’intérieur du polygone pol de forme complexe. Nous avons donc filtré spatialement les données de dem et nous avons assigné ce raster à la variable dem_ma que nous pouvons alors utiliser comme tout autre raster.
summary(getValues(dem_ma)) Min. 1st Qu. Median Mean 3rd Qu. Max.
100 221 259 270 304 839
NA's
38445
Terminons cette section sur les opérations de filtre par trois remarques importantes:
- L’étendue du raster retourné par la fonction
crop()sera différente de celle du raster initial (sauf si l’étendue initiale est utilisée pour rogner). À l’inverse, la fonctionmask()préserve l’étendue spatiale.
Vous pouvez en faire la vérification:
extent(dem)class : Extent
xmin : -72.72
xmax : -70.85
ymin : 45
ymax : 46.06 extent(dem_cr)class : Extent
xmin : -72
xmax : -71.5
ymin : 45.2
ymax : 45.8 extent(dem_ma)class : Extent
xmin : -72.72
xmax : -70.85
ymin : 45
ymax : 46.06
- Le temps de calcul pour réaliser l’opération
crop()est souvent très rapide, ce qui n’est pas le cas de l’opérationmask()quand le polygone est complexe. Il est parfois possible d’avoir des gains d’efficacité en faisant appel àcrop()avant d’utilisermask().
- Dans la situation où seules les valeurs des cellules filtrées nous intéresse, il est possible d’utiliser la fonction
extract()plutôt que la fonctionmask(). La fonctionextract()de la bibliothèquerasterretourne une liste pour laquelle chaque élément donne les valeurs des cellules extraites pour chaque couche du raster.
Par exemple, le raster dem possède une seule couche, ainsi la liste retournée par la fonction extract() ne possède qu’un seul élément. Toutefois, cet élément est un vecteur de taille 6075 listant la valeur de chacune des cellules extraites.
[1] 6075 Min. 1st Qu. Median Mean 3rd Qu. Max.
100 221 259 270 304 839 dem_ex <- extract(dem, pol)
length(dem_ex[[1]])
summary(dem_ex[[1]])8.1.2.3 Combiner des rasters
Une opération qui peut s’avérer utile est celle de combiner des rasters, c’est-à-dire former un seul raster à partir de deux rasters ou plus. Par exemple, une telle opération pourrait être nécessaire si, pour une problématique donnée, nous devions combiner des rasters d’élévation de chaque région administrative du Québec pour obtenir un seul raster couvrant l’entièreté de la province.
Fonction merge()
La fonction merge() de la bibliothèque raster permet de combiner deux rasters ou plus. Cette fonction s’utilise différemment de la fonction générale merge() vue au module 7 pour combiner des data frame.
En guise d’exemple, combinons les rasters dem_ma et dem_ma_inv créés plus haut en applicant la fonction mask() au raster dem :
dem_merge <- merge(dem_ma, dem_ma_inv)
Notez que pour combiner des rasters avec la fonction
merge()ceux-ci doivent avoir la même résolution et posséder le même système de coordonnées de référence (SCR).
Il est possible que deux rasters que l’on souhaite combiner couvrent certaines régions communes. C’est-à-dire que certains pixels se superposent. Si la valeur des pixels se superposant diffère, la fonction merge() choisira la valeur que prend le pixel dans le raster donné en premier argument.
Par exemple, créons un raster qui soit identique à dem_cr mais pour lequel tous les pixels ont une altitude 100 m plus grande :
#Ajoutons 100m à tous les pixels de dem_cr
dem_cr_plus <- dem_cr + 100Ensuite, combinons dem_cr_plus à dem_ma avec la fonction merge(). Le raster combiné prendra des valeurs différentes sur les pixels qui se superposent selon l’ordre des arguments :
dem_merge_ordre1 <- merge(dem_cr_plus, dem_ma)
dem_merge_ordre2 <- merge(dem_ma, dem_cr_plus)Fonction mosaic()
La fonction mosaic() de la bibliothèque raster est similaire à merge() mais offre plus de flexibilité pour définir la valeur des pixels qui se chevauchent. En particulier, elle possède un troisième argument servant à préciser la fonction avec laquelle la valeur des pixels redondants est calculée.
Par exemple, la fonction pourrait choisir la valeur la plus grande, la valeur la plus petite, ou encore la moyenne des valeurs. La fonction pourrait aussi être définie par l’usager et prendre une forme plus spécifique.
dem_mosaic_min <- mosaic(dem_cr_plus, dem_ma, fun = min)
dem_mosaic_max <- mosaic(dem_cr_plus, dem_ma, fun = max)
dem_mosaic_mean <- mosaic(dem_cr_plus, dem_ma, fun = mean)
La fonction mosaic() requiert également que les rasters utilisés possèdent la même résolution et le même SCR.
Il existe des bibliothèques spécialisées qui offrent des fonctions plus avancées pour le traitement des pixels aux frontières des rasters qui se chevauchent (par exemple les bibliothèques landsat et satellite). L’utilisation de ces méthodes dépasse toutefois les objectifs de ce cours.
8.1.3 Problématique à résoudre
Maintenant que nous avons appris les opérations de base pour manipuler les données matricielles, nous sommes en mesure de résoudre la problématique énoncée au début de cette leçon.
Résolution de la question 1
Rappelons la première question :
Parmi les quatre parcs nationaux de la région de Sherbrooke, lequel dispose du plus haut sommet?
Les étapes de la démarche de résolution sont les suivantes:
- S’assurer que le raster d’élévation
demet les données vectoriellesparcssont dans le même SCR.- Utiliser la fonction
mask()pour extraire les cellules dedemqui sont dans les parcs nationaux considérés,- Déterminer la valeur maximale d’élévation dans ce sous-ensemble de cellules extraites,
- Trouver les coordonnées spatiales associées à ce point de valeur d’élévation maximale.
- Déterminer dans quel parc se trouve les coordonnées spatiales du sommet le plus haut.
Commençons!
1. Vérication des SRC
Commençons par vérifier si les systèmes de coordonnées de référence (SCR) de dem et de parcs sont identiques:
st_crs(dem) == st_crs(parcs)[1] FALSEPuisque les SCR diffèrent, nous allons reprojeter le raster dem en utilisant le SCR de parcs en utilisant la fonction projectRaster(). Nous avons déjà réalisé cette opération à la section précédente et nous reprenons donc ci-dessous la ligne de commande vue plus haut :
dem_lcc <- projectRaster(dem, crs = crs(parcs))
Pour les prochaines manipulations, nous utiliserons donc dem_lcc et parcs.
2. Filtrer le raster dem
Nous cherchons ensuite à filtrer les cellules du raster d’élévation dem pour extraire celles situées à l’intérieur des limites de l’un ou de l’autre des quatre parcs nationaux considérés. Le shapefile parcs contient justement les polygones délimitant les quatre parcs. Nous pouvons donc appliquer la fonction mask() au raster dem en utilisant directement le shapefile parcs en second argument.
dem_parcs <- mask(dem_lcc, parcs)
mapview(dem_parcs)Le raster dem_parcs obtenu par l’opération mask() possède la même étendue que le raster original dem_lcc mais ses valeurs diffèrent. Les cellules de dem_parcs prennent la valeur NA partout sauf à l’intérieur des quatre parcs nationaux où elles prennent alors la même valeur que la cellule correspondante dans dem_lcc.
3. Trouver l’élévation maximale
Nous pouvons maintenant trouver la valeur d’élévation la plus élevée en utilisant la fonction getValues() suivie de la fonction max().
vmax <- max(getValues(dem_parcs), na.rm = TRUE)
vmax[1] 1083
Nous avons ainsi obtenu l’élévation maximale de ces parcs qui est de 1083 m. Nous cherchons alors les coordonnées spatiales associées à cette valeur. Nous pouvons faire appel à la fonction which() pour trouver l’indice de la cellule (ou les indices des cellules, s’il y en a plusieurs) en question.
ind_max <- which(getValues(dem_parcs) == max(getValues(dem_parcs), na.rm = TRUE))
ind_max [1] 31561
Notons qu’il existe une fonction pour identifier le maximum, which.max(), qui réalise la même opération mais requiert une syntaxe un peu plus simple.
which.max(getValues(dem_parcs))[1] 315614. Déterminer les coordonnées du plus haut sommet
Pour déterminer les coordonnées de la cellule identifiée nous utilisons l’indice ind_max et la fonction as.data.frame() avec xy = TRUE et centroid = TRUE comme vu au module 5 :
df_max <- as.data.frame(dem_parcs[ind_max, drop = FALSE], xy = TRUE, centroid = TRUE, na.rm = TRUE)
df_max x y layer
1 -207329 165880 1083Deux remarques méritent d’être mentionnées concernant cette opération :
- L’argument
drop = FALSEpermet d’éviter queRne convertissedem_parcs[ind_max, ]en un vecteur, c’est important car nous voulons conserver sa forme matricielle.
na.rm = TRUEpermet d’ignorer toutes les valeurs masquées, comme nous l’avons dans d’autres fonctions (e.g.mean()).
v. Déterminer le parc possédant le point d’élévation maximale
Une fois isolées, les coordonnées x et y du pixel d’élévation maximale peuvent être utilisées pour créer un objet spatial de classe sf contenant le centroïde de ce pixel grâce à la fonction st_as_sf(). Nous nous servirons par la suite de ce point pour visualiser sa position et déterminer dans quel parc national il est situé.
sf_point_max <- st_as_sf(df_max, coords = c("x", "y"),
crs = st_crs(dem_parcs))
sf_point_maxSimple feature collection with 1 feature and 1 field
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -207300 ymin: 165900 xmax: -207300 ymax: 165900
Projected CRS: NAD83 / Quebec Lambert
layer geometry
1 1083 POINT (-207329 165880)
Remarquez que nous avons attribué à ce point le même SRC que celui du raster dem_parcs().
En superposant, avec mapview(), les trois couches d’informations spatiales que nous venons de manipuler, nous pouvons repérer le parc dans lequel se trouve ce point d’élévation maximale.
map_point <- mapview(dem_parcs) + mapview(parcs, alpha = 0.01) + mapview(sf_point_max, col.regions = "red")
map_point@mapFIGURE 8.1: En cliquant sur le polygone du parc contenant le point rouge (point d’élévation maximal), il est possible de constater que le point se retrouve dans le Parc national du Mont-Mégantic
Nous constatons que ce point est situé dans le Parc national du Mont-Mégantic. Au lieu de déduire sa localisation de manière visuelle, nous allons à présent réaliser une opération topologique pour isoler le polygone du parc abritant ce plus haut sommet. Pour ce faire, nous utilisons la fonction st_intersects() étudiée au module 7. Rappelons que cette fonction retourne la valeur TRUE lorsque deux objets vectoriels se recoupent et FALSE autrement.
st_intersects(parcs, sf_point_max, sparse = FALSE) [,1]
[1,] FALSE
[2,] TRUE
[3,] FALSE
[4,] FALSENous utilisons ensuite ce vecteur logique pour identifier le parc auquel ce sommet appartient. Notez que le nom des parcs est donné par l’attribut TRQ_NM_.
parcs[st_intersects(parcs, sf_point_max, sparse = FALSE), ]$TRQ_NM_[1] "Parc national du Mont-Mégantic"Cette opération peut être écrite plus simplement sous la forme:
parcs[sf_point_max, ]$TRQ_NM_[1] "Parc national du Mont-Mégantic"Cette dernière manipulation nous permet de répondre à notre première question:
parmi les quatre parcs nationaux sélectionnés, c’est le Parc national du Mont-Mégantic qui a le plus haut sommet, sommet qui culmine à 1083 m d’altitude!
Résolution de la question 2
Nous allons maintenant répondre à la deuxième question de notre problématique:
Quel est le profil topographique du sentier se rendant au plus proche de ce sommet?
Nous allons nous placer dans la situation suivante : nous désirons faire une randonnée pédestre jusqu’au sommet que nous venons d’identifier (à tout le moins, le plus proche possible de ce sommet). Afin de nous faire une idée précise de l’effort physique que nous devrons fournir lors de cette randonnée, nous allons réaliser un profil topographique du sentier se rendant au plus proche de ce sommet.
La figure 8.2 donne un exemple de profil topographique pour le sentier de la grande traversée dans le Parc national de la Gaspésie.
](Module8/images/8_Profil_ex.png)
FIGURE 8.2: Exemple de profil topographique: le sentier international des Appalaches taille réelle
Voici les étapes que nous allons suivre en vue de répondre à la question posée:
- Créer un shapefile du Parc national du Mont-Mégantic,
parc_megantic, à partir deparcs.- Importer les données des sentiers estivaux de la SEPAQ et des données d’élévation plus précises.
- S’assurer que les nouveaux objets importés et
parc_meganticont le même SCR.- Isoler les sentiers estivaux du Parc national du Mont-Mégantic.
- Trouver le chemin le plus proche du sommet identifié à la question 1.
- Extraire les cellules d’élévation de
dem_lccsur ce sentier.- Réaliser un profil d’élévation.
Commençons!
1. Créer un shapefile du Parc national du Mont-Mégantic
Puisque le profil topographique que nous désirons créer se situe à l’intérieur du Parc national du Mont-Mégantic, isolons le polygone constituant ce parc à partir du shapefile parcs regroupant les quatre parcs. Rappelons que le Parc national du Mont-Mégantic est celui qui possède le plus haut sommet. En nous basant sur les commandes réalisées plus haut, nous pouvons définir le shapefile parc_megantic de la façon suivante:
parc_megantic <- parcs[st_intersects(parcs, sf_point_max, sparse = FALSE), ]
# Ou plus simplement:
# parc_megantic <- parcs[sf_point_max, ]2. Importer les données
Maintenant importons les données vectorielles pour tous les sentiers de la SÉPAQ. Ce shapefile se trouve dans le dossier Module8_donnees que vous avez téléchargé au début de la leçon :
sentiers <- st_read("Module8/Module8_donnees/sentiers_sepaq/Sentier_ete_l.shp")Reading layer `Sentier_ete_l' from data source
`D:\Dropbox\Teluq\Enseignement\Cours\SCI1031\Developpement\Structure_test\sci1031\Module8\Module8_donnees\sentiers_sepaq\Sentier_ete_l.shp'
using driver `ESRI Shapefile'
Simple feature collection with 3606 features and 22 fields
Geometry type: MULTILINESTRING
Dimension: XY
Bounding box: xmin: -822400 ymin: 150300 xmax: 437600 ymax: 689800
Projected CRS: NAD83 / Quebec Lambertmapview(sentiers)