5.1 Leçon
5.1.1 Télécharger les données
Dans les sections 5.1.5 à 5.1.10 ainsi que dans la section exercices du présent module, vous apprendrez à lire et visualiser des données déjà existantes. Afin de faciliter le téléchargement de ces multiples données, l’ensemble des couches d’informations spatiales peuvent être téléchargées en cliquant sur un seul lien: données pour le module 5. Sauvegardez le dossier compressé (zip) dans votre répertoire de travail Module5_donnees pour ce module, et dézippez-le. Le dossier comprend quatre fichiers tif:
Temp_vdq.tifLandsat_LaTuque.tifCouvert_2001.tifCouvert_2016.tif
Les données matricielles Temp_vdq.tif présentent la température de surface sur le territoire de la ville de Québec.
Le fichier Landsat_LaTuque.tif contient des données captées par le satellite Landsat sur une section du territoire de la Haute Mauricie, près de la ville de La Tuque.
Les données Couvert_2001.tif et Couvert_2016.tif correspondent à la couverture terrestre (p. ex. forêt, champ, eau, etc.) d’une petite région du Colorado aux années 2001 et 2016. Ces données sont utilisées dans la section exercices.
5.1.2 Créer des données matricielles
Les données matricielles représentent la surface terrestre par une grille régulière, communément appelée un raster. Dans cette leçon, nous utiliserons les expressions «raster» et «données matricielles» de façon interchangeable.
Pour créer, lire et manipuler des données matricielles, nous allons utiliser la bibliothèque raster. Commençons par charger la bibliothèque raster dans notre session de travail R.
# Installez la bibliothèque si ce n'est pas déjà fait
# install.packages("raster")
# Chargez la bibliothèque
library(raster)Créer un raster simple et le visualiser
Au module 2, nous avons expliqué qu’un raster est formé de rectangles de même forme et de même dimension appelés cellules ou pixels. À chaque cellule de cette matrice correspond une valeur numérique (ou une valeur manquante) associée à un attribut d’intérêt. On appelle couche (« layer » en anglais) l’information recueillie dans la matrice.
La fonction raster() de la bibliothèque raster permet de créer un raster. Par exemple:
M <- raster(nrows=8, ncols=8, xmn = 1, xmx = 5, ymn = 1, ymx = 5, vals = 1:64)Où nrows et ncols correspondent respectivement au nombre de lignes et au nombre de colonnes du raster M, xmn et xmx correspondent respectivement aux coordonnées-x minimale et maximale du raster, ymn et ymx aux coordonnées-y minimale et maximale, et vals est un vecteur comprenant la valeur de chaque pixel du raster. Dans le cas présent, le raster M contient 64 pixels. Le premier pixel a la valeur 1, le deuxième pixel a la valeur 2 et ainsi de suite.
Voyons les informations données, lorsque nous appelons le raster M que nous venons de créer:
Mclass : RasterLayer
dimensions : 8, 8, 64 (nrow, ncol, ncell)
resolution : 0.5, 0.5 (x, y)
extent : 1, 5, 1, 5 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
source : memory
names : layer
values : 1, 64 (min, max)Nous remarquons que des informations additionnelles apparaissent: ncell correspond au nombre de cellules (ou de pixels) dans le raster, resolution correspond à la résolution des pixels, extent correspond à l’étendue du raster définie par ses coordonnées maximales et minimales, et crs correspond aux paramètres du système de coordonnées de référence utilisé.
Si le SCR d’un raster n’est pas défini au moment de sa création, comme dans le cas présent, alors le SCR WGS84 sera attribué par défaut.
Remarquez que la classe (class) de l’objet M est définie comme étant un RasterLayer. Nous verrons dans la dernière section de cette leçon qu’il existe d’autres classes de raster, soit les RasterBrick et les RasterStack.
Remarquez aussi que la résolution d’un pixel est de 0.5 x 0.5, car les 64 pixels du raster occupent le carré d’aire 16 délimité par les quatre points (1,1), (1,5), (5,1) et (5,5).
Ainsi, une façon équivalente de créer le raster M est:
M <- raster(res = 0.5, xmn = 1, xmx = 5, ymn = 1, ymx = 5, vals = 1:64)
Mclass : RasterLayer
dimensions : 8, 8, 64 (nrow, ncol, ncell)
resolution : 0.5, 0.5 (x, y)
extent : 1, 5, 1, 5 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
source : memory
names : layer
values : 1, 64 (min, max)Dans cette notation, nous avons spécifié la résolution et non la dimension du raster.
Nous pouvons également connaître les paramètres d’un raster en utilisant les fonctions correspondantes.
dim(M)
[1] 8 8 1
ncell(M)
[1] 64
nrow(M)
[1] 8
ncol(M)
[1] 8
res(M)
[1] 0.5 0.5
extent(M)
class : Extent
xmin : 1
xmax : 5
ymin : 1
ymax : 5
crs(M)
Coordinate Reference System:
Deprecated Proj.4 representation: +proj=longlat +datum=WGS84 +no_defs
WKT2 2019 representation:
GEOGCRS["unknown",
DATUM["World Geodetic System 1984",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]],
ID["EPSG",6326]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8901]],
CS[ellipsoidal,2],
AXIS["longitude",east,
ORDER[1],
ANGLEUNIT["degree",0.0174532925199433,
ID["EPSG",9122]]],
AXIS["latitude",north,
ORDER[2],
ANGLEUNIT["degree",0.0174532925199433,
ID["EPSG",9122]]]] Il existe plusieurs fonctions permettant de visualiser les rasters.
Nous pouvons simplement utiliser la fonction plot().
plot(M)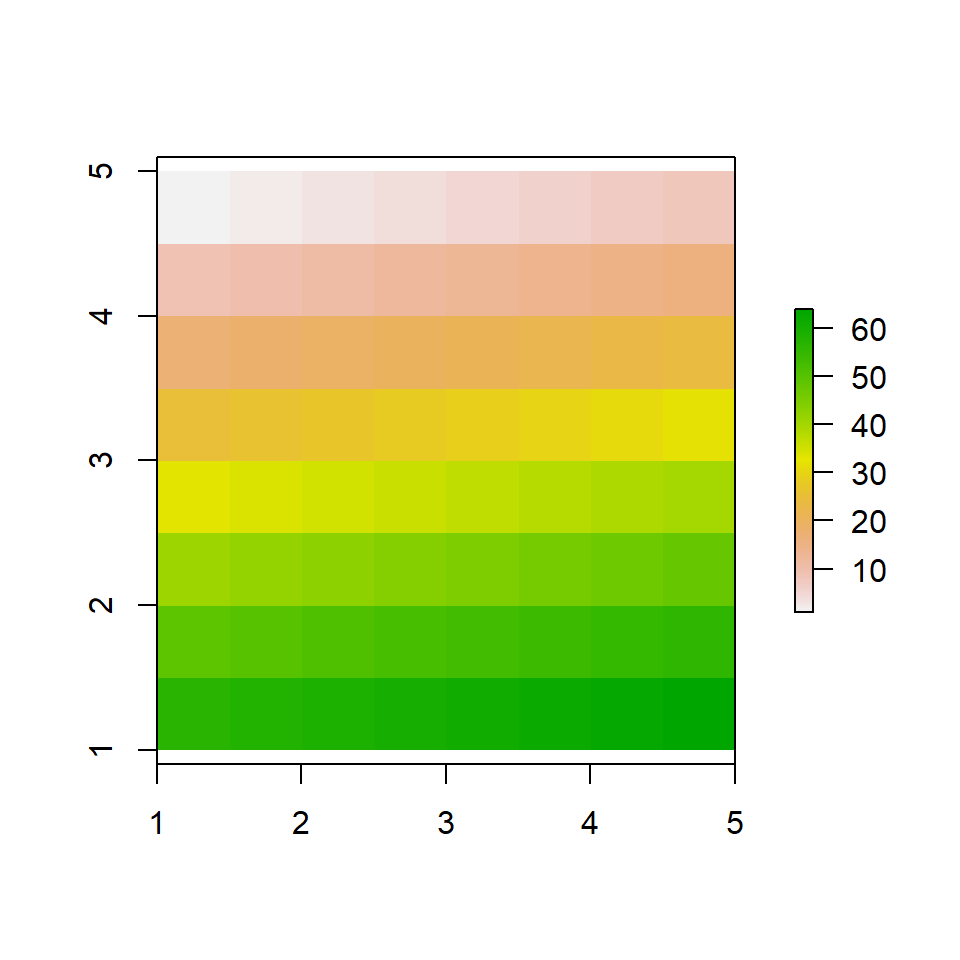
FIGURE 5.1: Visualisation du raster M avec la fonction plot()
Nous pouvons aussi utiliser la fonction mapview() de la bibliothèque mapview:
library(mapview)
library(leaflet)
mapview(M)
FIGURE 5.2: Visualisation du raster M avec la fonction mapview()
Nous avons une certaine préférence pour l’esthétique qu’offre mapview(), n’est-ce pas?
Peu importe la fonction choisie, celle-ci transforme la valeur de chaque cellule en couleur. Différentes palettes de couleur peuvent être utilisées, mais pour l’instant, limitons-nous à la palette de couleur par défaut, qui est inferno de la bibliothèque viridis, inclue automatiquement dans la bibliothèque mapview.
Remarquez que le premier pixel, qui porte la valeur 1 dans le cas présent, se trouve en haut à gauche. Le dernier pixel, quant à lui, se trouve dans le coin inférieur droit. L’identité des pixels suit donc les lignes d’un raster.
Raster de différents types de données
Les rasters peuvent prendre des valeurs de type discrètes (integer) et des nombres réels (numeric).
Ils peuvent également prendre des valeurs logiques (logical). Par exemple, remplaçons les valeurs discrètes du raster M défini plus haut par des valeurs logiques.
z <- 1:64
class(z) #la fonction class() renvoie le type de données de l'objet z[1] "integer"# Créons un nombre logique qui est vrai lorsque z est un multiple de trois, et faux autrement
z_mult3 <- z %% 3 == 0
# La fonction modulo, s'exprime par le symbole %%,
# L'expression x %% y vaut 0 si y est un multiple de x,
# L'expression x %% y vaut r si y n'est pas un multiple de x.
# r correspond alors au reste de la division x/y
z_mult3 [1] FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE
[9] TRUE FALSE FALSE TRUE FALSE FALSE TRUE FALSE
[17] FALSE TRUE FALSE FALSE TRUE FALSE FALSE TRUE
[25] FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE
[33] TRUE FALSE FALSE TRUE FALSE FALSE TRUE FALSE
[41] FALSE TRUE FALSE FALSE TRUE FALSE FALSE TRUE
[49] FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE
[57] TRUE FALSE FALSE TRUE FALSE FALSE TRUE FALSEclass(z_mult3) #vérifions que les valeurs sont bien de type logique[1] "logical"# utilisons le vecteur logique z_mult3 pour créer un raster logique
M_logique <- raster(nrows = 8, ncols = 8, xmn = 1, xmx = 5, ymn = 1, ymx = 5,
vals = z_mult3)
M_logiqueclass : RasterLayer
dimensions : 8, 8, 64 (nrow, ncol, ncell)
resolution : 0.5, 0.5 (x, y)
extent : 1, 5, 1, 5 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
source : memory
names : layer
values : 0, 1 (min, max)Visualisons maintenant ce raster de type logique:
FIGURE 5.3: Raster dont les valeurs sont de type logique
Les rasters ne peuvent pas prendre des valeurs de type caractères (character) mais ils peuvent tout de même prendre des valeurs catégoriques.
Petit rappel, avec R, les données catégoriques sont représentées par des données de type facteurs (factor). Plus précisément, les données catégoriques sont emmagasinées comme étant des nombres entiers auxquels sont associées des étiquettes - des identifiants uniques. Nous référons à ces identifiants comme étant des niveaux (levels). Par exemple:
# Définissons un vecteur de caractères
mois_hiver <- c("décembre", "janvier", "février", "mars")
# Ce vecteur est bel et bien de type caractère
class(mois_hiver)[1] "character"# Maintenant transformons ce vecteur en vecteur de type facteur
mois_hiver_facteur <- factor(mois_hiver)
# Ce vecteur transformé est bien de type facteur
class(mois_hiver_facteur)[1] "factor"# Ce nouveau vecteur possède 4 niveaux différents
mois_hiver_facteur[1] décembre janvier février mars
Levels: décembre février janvier mars# ou encore
levels(mois_hiver_facteur)[1] "décembre" "février" "janvier" "mars" Revenons maintenant aux rasters. Reprenons l’exemple du raster des multiples de 3. Nous allons le transformer en raster de type facteur.
# Nous transformons d'abord le vecteur z de nombres entiers de 1 à 64,
# en vecteur de type caractère
z_char <- z
z_char[z%%3 == 0] <- "Multiple de 3"
z_char[z%%3 != 0] <- "Autre"
class(z_char)[1] "character"# Transformons le vecteur z_char en vecteur de type facteur
z_fact <- factor(z_char)
class(z_fact)[1] "factor"# Obtenons maintenant un raster de type facteur
M_factor <- raster(nrows = 8, ncols = 8, xmn = 1, xmx = 5, ymn = 1, ymx = 5,
vals = z_fact)
M_factorclass : RasterLayer
dimensions : 8, 8, 64 (nrow, ncol, ncell)
resolution : 0.5, 0.5 (x, y)
extent : 1, 5, 1, 5 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
source : memory
names : layer
values : 1, 2 (min, max)
attributes :
ID VALUE
1 Autre
2 Multiple de 3Visualisons maintenant ce raster de type facteur:
mapview(M_factor)FIGURE 5.4: Raster dont les valeurs sont de type facteur
5.1.3 Comprendre la structure d’un raster
Les objets de type raster disposent d’une structure d’objet particulière. Si l’on veut accéder aux valeurs stockées, on doit procéder d’une certaine manière.
La valeur d’une cellule peut être obtenue en référant à l’identifiant (indice) de son pixel; c’est-à-dire un numéro entre 1 et le nombre total de cellules, ncell, dans le raster.
La valeur d’une cellule peut aussi être obtenue en référant à sa position (ligne, colonne) dans sa structure matricielle.
Par exemple, considérons le raster G suivant, de dimensions 5 par 5, former de nombres aléatoires entre 0 et 1.
class : RasterLayer
dimensions : 5, 5, 25 (nrow, ncol, ncell)
resolution : 0.5, 0.5 (x, y)
extent : 1, 3.5, 1, 3.5 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
source : memory
names : layer
values : 0.1, 1 (min, max)La figure suivante illustre comment les cellules sont indexées et positionnées dans un raster. La cellule supérieure gauche, de position [1,1] est toujours celle portant l’indice 1.
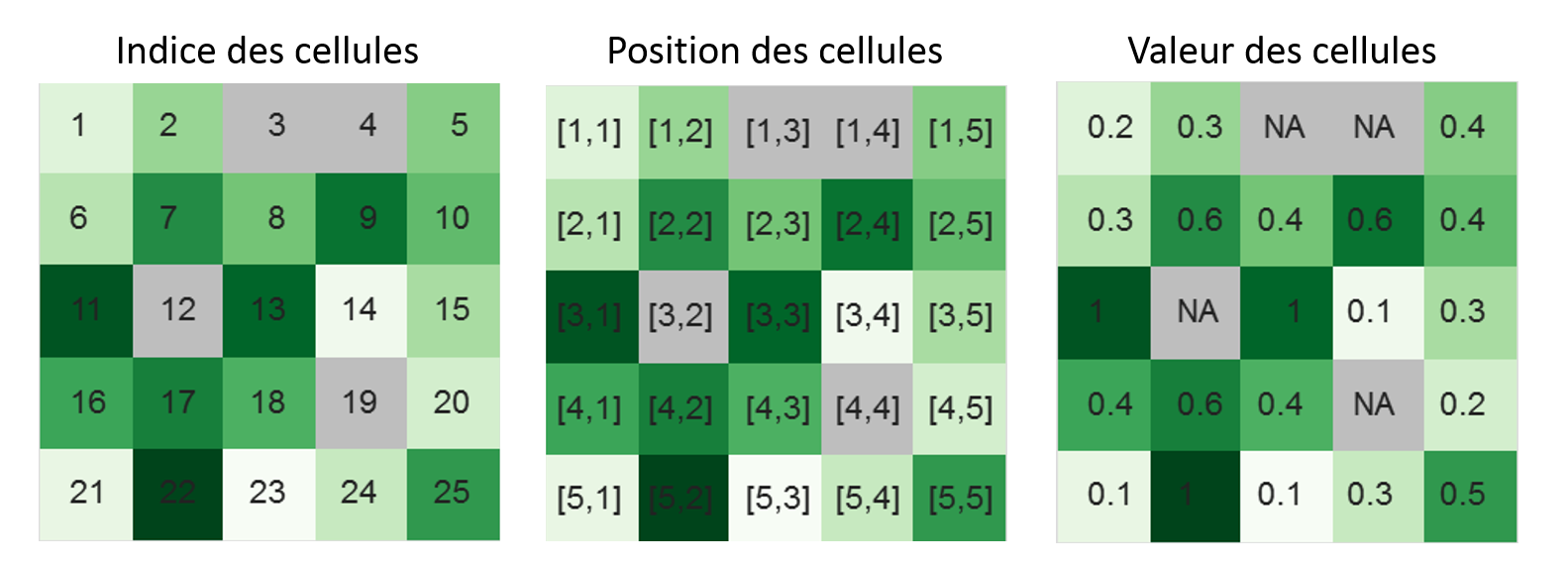
FIGURE 5.5: Structure d’un raster: indice, position et valeur des pixels
Ainsi, pour accéder à des valeurs spécifiques du raster, on procède de la façon suivante:
# Accéder à la première valeur
G[1]
[1] 0.2
# Accéder à la valeur de la cellule à la position (3,2)
G[3, 2]
[1] NA
# Accéder aux valeurs de 5 à 10
G[5:10]
[1] 0.4 0.3 0.6 0.4 0.6 0.4
# Accéder à des valeurs spécifiques
G[c(7, 13, 17:20)]
[1] 0.6 1.0 0.6 0.4 NA 0.2Il est souvent plus simple d’utiliser l’indice lorsque nous voulons accéder aux valeurs de plusieurs cellules. Par ailleurs, l’utilisation de la position est souvent plus intuitive.
Notons toutefois qu’il peut être dangereux d’extraire des valeurs en utilisant les indices des cellules. En effet, nous perdons une information précieuse: la localisation de la cellule dans l’espace; c’est-à-dire ses coordonnées X et Y. C’est pourquoi, il est souvent privilégié de convertir le raster en data.frame. La fonction as.data.frame(..., xy = TRUE), appliquée à un objet de classe raster, présente l’avantage de retourner les coordonnées associées à l’indice.
G_df <- as.data.frame(G, xy = TRUE)
head(G_df) x y layer
1 1.25 3.25 0.2
2 1.75 3.25 0.3
3 2.25 3.25 NA
4 2.75 3.25 NA
5 3.25 3.25 0.4
6 1.25 2.75 0.3Ainsi, en référant à l’indice d’une cellule, nous pouvons connaître non seulement sa valeur mais aussi sa localisation dans l’espace.
G_df[13, ] x y layer
13 2.25 2.25 1Notez que par défaut, la coordonnée renvoyée par la fonction as.data.frame() correspond au coin inférieur gauche de chaque pixel. Il est cependant possible de renvoyer le centroïde du pixel en utilisant l’argument as.data.frame(..., xy = TRUE, centroids = TRUE).
FIGURE 5.6: (A) Coordonnées renvoyées par défaut par la fonction as.data.frame; (B) Coordonnées des centroïdes des pixels renvoyées lorsque l’argument centroids = TRUE est utilisé dans la fonction as.data.frame
5.1.4 Statistiques de base sur un raster
Voyons maintenant comment calculer des statistiques de base sur les valeurs contenues dans un raster.
Tout d’abord, pour connaître l’ensemble des valeurs d’un raster, nous pouvons utiliser la fonction getValues().
getValues(G) [1] 0.2 0.3 NA NA 0.4 0.3 0.6 0.4 0.6 0.4 1.0 NA
[13] 1.0 0.1 0.3 0.4 0.6 0.4 NA 0.2 0.1 1.0 0.1 0.3
[25] 0.5Cette fonction est équivalente à :
G[] [1] 0.2 0.3 NA NA 0.4 0.3 0.6 0.4 0.6 0.4 1.0 NA
[13] 1.0 0.1 0.3 0.4 0.6 0.4 NA 0.2 0.1 1.0 0.1 0.3
[25] 0.5Nous pouvons alors calculer des statistiques élémentaires sur ces valeurs. Par exemple, quelle est la valeur maximale du raster G?
max(getValues(G), na.rm = TRUE)[1] 1Noter que nous devons préciser que les valeurs NA ne soient pas prises en considération lors du calcul de statistiques. En effet, na.rm = TRUE signifie que les valeurs NA sont retirées (remove en anglais, abrégé par rm).
Plus simplement, nous pouvons utiliser la fonction équivalente maxValue exclusive aux données de classe raster.
maxValue(G)[1] 1De la même façon, nous pouvons obtenir d’autres statistiques élémentaires:
minValue(G)
[1] 0.1
min(getValues(G), na.rm = TRUE)
[1] 0.1
mean(getValues(G), na.rm = TRUE)
[1] 0.4381
median(getValues(G), na.rm = TRUE)
[1] 0.4
quantile(getValues(G), na.rm = TRUE)
0% 25% 50% 75% 100%
0.1 0.3 0.4 0.6 1.0 La fonction summary() permet d’obtenir plusieurs statistiques:
summary(G) layer
Min. 0.1
1st Qu. 0.3
Median 0.4
3rd Qu. 0.6
Max. 1.0
NA's 4.0En plus du minimum, du maximum, et de la médiane, la fonction summary() retourne le premier et le troisième quantile, ainsi que le nombre de cellules de valeur NA contenu dans le raster.
La fonction cellStats permet également d’obtenir des statistiques sur les rasters. La statistique désirée doit être précisée dans les options de la fonction cellStats. Par exemple:
cellStats(G, mean, na.rm = TRUE)
[1] 0.4381
cellStats(G, sd, na.rm = TRUE) #la déviation standard
[1] 0.2801
cellStats(G, max, na.rm = TRUE)
[1] 1
cellStats(G, min, na.rm = TRUE)
[1] 0.1
cellStats(G, median, na.rm = TRUE)
[1] 0.4
cellStats(G, quantile, na.rm = TRUE)
0% 25% 50% 75% 100%
0.1 0.3 0.4 0.6 1.0
cellStats(G, range, na.rm = TRUE) #le minimum et le maximum
[1] 0.1 1.0
cellStats(G, sum, na.rm = TRUE)
[1] 9.2Nous pouvons également visualiser la distribution des valeurs contenues dans un raster en utilisant les fonctions R usuelles telles que hist() ou boxplot. Par exemple,
hist(G,
main = "",
xlab = "Valeurs",
ylab = "Fréquence",
col = "darkorange")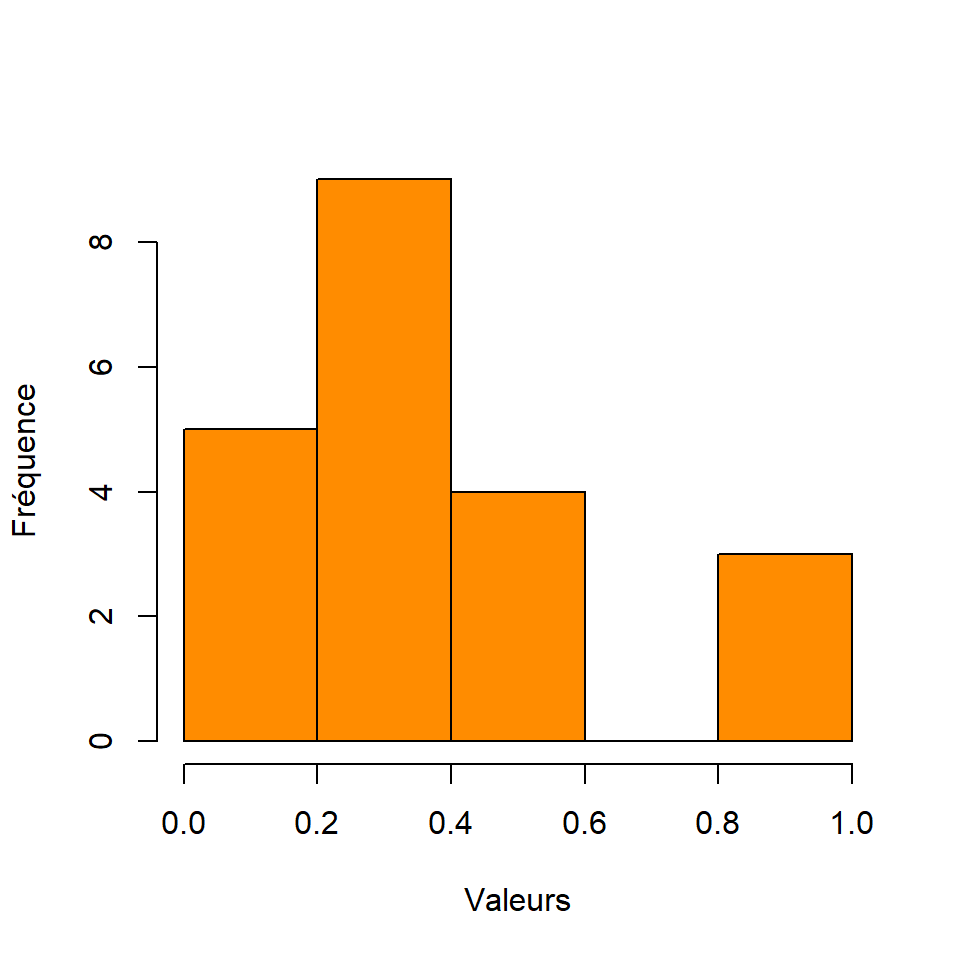
FIGURE 5.7: Histogramme de la distribution des valeurs dans le raster G
Ou encore,
boxplot(G,
main = "",
ylab = "Valeurs",
col = "darkorange")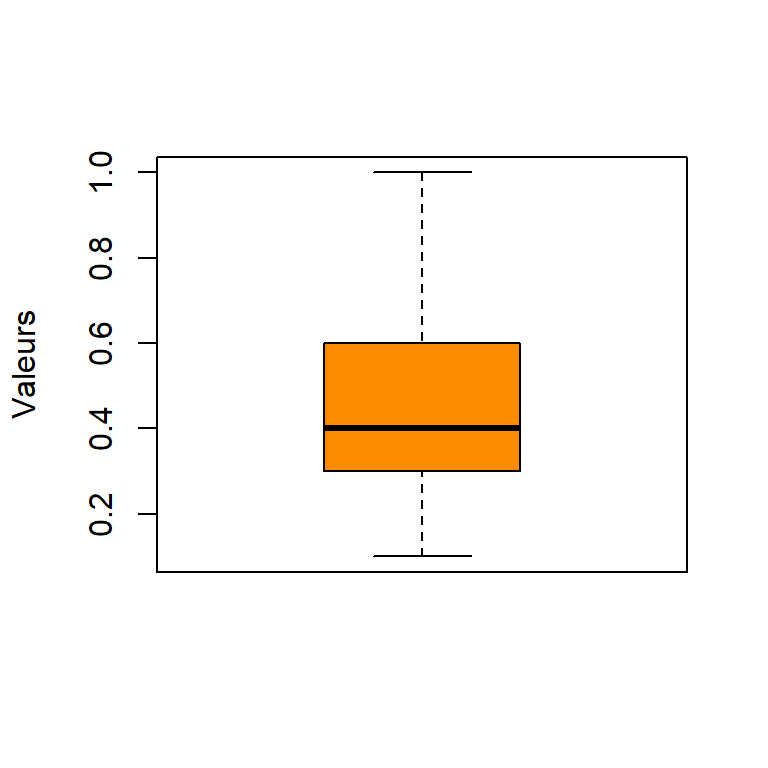
FIGURE 5.8: Valeur moyenne et intervalle de confiance du raster G
5.1.5 Lire un raster et explorer son contenu
Dans les sections précédentes, nous avons créé et manipulé des rasters très simples et peu volumineux. Dans cette section, nous manipulerons un raster plus substantiel, constitué de données réelles sur les îlots de chaleur urbains.
Les îlots de chaleur urbains (ICU) sont des “zones urbaines où les températures sont plus chaudes que dans la région rurale voisine” (Santé Canada 2020). Les ICU amplifient les effets négatifs sur la santé humaine pendant les vagues de chaleur. Les ICU se produisent surtout dans les zones où les humains ont fortement altéré le couvert du sol, par exemple pour y aménager des infrastructures en béton (bâtiments, stationnement, route, etc.). L’absence de végétation, la présence de surfaces imperméables et non-réfléchissantes contribuent à la formation d’ICU (Santé Canada 2020).
La température de surface mesurée sur les territoires urbains permet d’identifier la présence d’îlots de chaleur33. Les données sur les ICU pour l’ensemble du territoire québécois sont disponibles sur le site gouvernemental Données Québec en format GeoTIFF. Puisque cette base de données spatiales est particulièrement volumineuse, nous allons travailler seulement avec les données matricielles relatives à la région de la ville de Québec.
Lire les données
Nous allons maintenant lire les données matricielles en utilisant la fonction raster() de la bibliothèque raster.
T_vdq <- raster("Module5/Module5_donnees/Temp_vdq.tif")Nous pouvons d’emblée reconnaître les informations relatives à la dimension, la résolution, l’étendue, le CRS, et aux valeurs minimale et maximale du raster T_vdq.
Nous pouvons également utiliser les fonctions dim(), ncell(), res(), extent(), crs(), et cellStats(, range) pour retrouver ces informations:
dim(T_vdq)[1] 857 860 1ncell(T_vdq)[1] 737020res(T_vdq)[1] 40 40extent(T_vdq)class : Extent
xmin : -230083
xmax : -195683
ymin : 300611
ymax : 334891 cellStats(T_vdq, range)[1] 1 9crs(T_vdq)Coordinate Reference System:
Deprecated Proj.4 representation:
+proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=46
+lat_2=60 +x_0=0 +y_0=0 +datum=NAD83 +units=m
+no_defs
WKT2 2019 representation:
PROJCRS["unknown",
BASEGEOGCRS["unknown",
DATUM["North American Datum 1983",
ELLIPSOID["GRS 1980",6378137,298.257222101,
LENGTHUNIT["metre",1]],
ID["EPSG",6269]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8901]]],
CONVERSION["unknown",
METHOD["Lambert Conic Conformal (2SP)",
ID["EPSG",9802]],
PARAMETER["Latitude of false origin",44,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8821]],
PARAMETER["Longitude of false origin",-68.5,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8822]],
PARAMETER["Latitude of 1st standard parallel",46,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8823]],
PARAMETER["Latitude of 2nd standard parallel",60,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8824]],
PARAMETER["Easting at false origin",0,
LENGTHUNIT["metre",1],
ID["EPSG",8826]],
PARAMETER["Northing at false origin",0,
LENGTHUNIT["metre",1],
ID["EPSG",8827]]],
CS[Cartesian,2],
AXIS["(E)",east,
ORDER[1],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]],
AXIS["(N)",north,
ORDER[2],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]]] Le nom de la couche de données matricielles contenue dans ce raster, c’est-à-dire son attribut, est obtenu en utilisant la fonction names().
names(T_vdq)[1] "Temp_vdq"Nous pouvons changer ce nom pour un nouveau:
names(T_vdq) <- "ICU"
T_vdqclass : RasterLayer
dimensions : 857, 860, 737020 (nrow, ncol, ncell)
resolution : 40, 40 (x, y)
extent : -230083, -195683, 300611, 334891 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=46 +lat_2=60 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs
source : Temp_vdq.tif
names : ICU
values : 1, 9 (min, max)Explorer les statistiques de base
Utilisons la fonction summary() pour déterminer les statistiques de base du raster T_vdq:
summary(T_vdq)Warning in .local(object, ...): summary is an estimate based on a sample of 1e+05 cells (13.57% of all cells) ICU
Min. 1.00
1st Qu. 2.00
Median 3.75
3rd Qu. 6.25
Max. 9.00
NA's 310116.00Remarquez le message retourné par R: “summary is an estimate based on a sample of 1e+05 cells (3.39% of all cells)”. Ce message nous prévient que, par défaut, les calculs de la fonction summary() sont réalisés sur un échantillon de 100 000 cellules choisies aléatoirement. Dans le cas présent, puisque le raster T_vdq contient ncells(T_vdq) = 2946366 cellules, un échantillon de 100 000 cellules correspond donc seulement à 3.39% de toutes les cellules.
La limite par défaut du nombre de cellules sélectionnées pour calculer les statistiques dans la fonction summary() est très utile pour obtenir des résultats rapides, surtout lorsque raster est volumineux. Cependant, dans certains cas, cet échantillonnage limité pourrait mener à un estimé trompeur. Ainsi, il est toujours possible de spécifier la taille désirée de l’échantillon en utilisant l’option maxsamp. Par exemple :
summary(T_vdq, maxsamp = ncell(T_vdq)) ICU
Min. 1.00
1st Qu. 2.00
Median 3.75
3rd Qu. 6.25
Max. 9.00
NA's 311157.00Vous remarquerez que l’exécution de la fonction summary() peut prendre plus de temps lorsque le nombre de cellules échantillonnées est plus grand. Dans le cas présent du raster T_vdq, les statistiques demeurent inchangées mais le nombre de valeurs NA a été corrigé.
Nous pouvons également visualiser l’histogramme des valeurs de température de surface.
hist(getValues(T_vdq),
breaks = 10,
main = "",
xlab = "Valeurs",
ylab = "Fréquence",
col = "darkorange")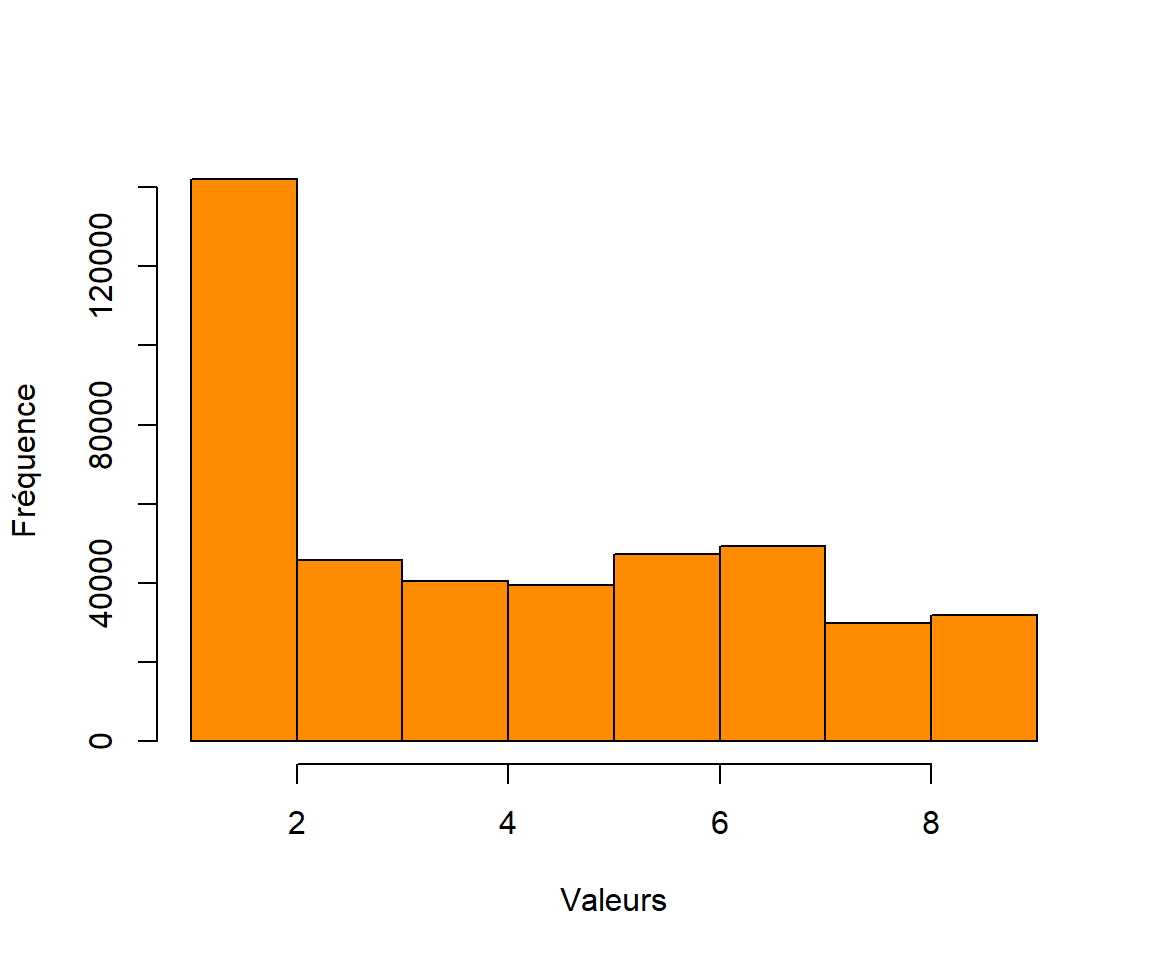
FIGURE 5.9: Distribution des températures de surface dans la ville de Québec
Remarquez que nous avons spécifié que la distribution soit calculée sur l’ensemble des valeurs contenues dans le raster T_vdq en utilisant la fonction getValues(). Autrement, la fonction hist() appliquée à un raster utilise un échantillonnage aléatoire de 100 000 cellules, similairement à la fonction summary().
5.1.6 Visualiser les données matricielles avec mapview()
Nous allons visualiser la carte des températures de surface de la région de la ville de Québec en utilisant la fonction mapview().
Afin de situer plus facilement la région illustrée sur le territoire du Québec, nous allons demander d’ajouter la carte d’OpenStreetMap34 comme carte de fonds.
mapview(T_vdq,
map.types = "OpenStreetMap",
legend = TRUE,
layer.name = 'ICU')FIGURE 5.10: Carte de la température de surface dans la ville de Québec
L’échelle de la légende indique des niveaux de température. Le niveau 1 correspond aux températures les plus fraîches, et le niveau 9 aux températures les plus chaudes.
Vous remarquerez que la résolution de cette carte n’est pas parfaite. En effet, par défaut, la fonction mapview() appliquée à un raster utilise 500 000 pixels. Pour que l’ensemble des pixels soient pris en compte, nous devons le préciser en définissant l’option maxpixels.
mapview(T_vdq, maxpixels = ncell(T_vdq),
map.types = "OpenStreetMap",
legend = TRUE,
layer.name = 'ICU')FIGURE 5.11: Carte de la température de surface dans la ville de Québec (visualisation de tous les pixels)
Naturellement, le temps nécessaire pour générer la carte est alors plus long.
Visualiser une section d’un raster
Nous voulons maintenant nous concentrer sur une petite section de la carte de la région de la ville de Québec. Nous pouvons le faire en spécifiant les lignes et les colonnes qui nous intéressent dans le raster. Par exemple, choisissons une région carrée de 100 x 100 cellules dans le quartier Sainte-Foy.
T_sec <- T_vdq[351:450, 351:450, drop = FALSE]
mapview(T_sec, map.types = "OpenStreetMap")FIGURE 5.12: Carte de la température de surface dans le secteur de Sainte-Foy
Notez que l’option drop = FALSE est importante car elle permet au nouvel objet T de demeurer un raster comme T_vdq. Autrement, T deviendrait un simple vecteur.
Nous observons sur la carte que les températures les plus chaudes (pixels de couleur jaune) sont situées sur les grandes infrastructures bétonnées comme les axes routiers ainsi que les bâtiments et les stationnements (par exemple ceux de la Place Laurier et Sainte-Foy). D’autre part, les températures les plus fraîches (pixels de couleur mauve foncé) sont situées sur des zones boisées comme celles sur le campus de l’Université Laval.
5.1.7 Changer la résolution d’un raster
Il est possible d’augmenter la résolution d’un raster. Cela peut s’avérer utile lorsque la résolution de ce dernier est trop petite (c’est-à-dire que la résolution est fine) pour exécuter rapidement des calculs sur celui-ci. Aussi, cela peut s’avérer utile lorsque nous devons travailler avec des rasters de résolution différente, il peut alors être nécessaire que tous les rasters aient la même résolution.
Pour augmenter la résolution d’un raster nous utilisons la fonction aggregate(). Nous devons alors spécifier le facteur, fact, par lequel nous voulons augmenter la résolution. Par exemple, fact = 4 augmentera la résolution par un facteur de \(4 * 4\). C’est-à-dire qu’une cellule de taille \(x * y\) aura, dans le nouveau raster, une taille \(4x * 4y\). Elle aura donc une taille 16 fois plus grande que dans le raster initial.
Quelle valeur prendra alors une cellule de plus grande résolution? Par défaut, la cellule aura comme valeur la moyenne des valeurs des cellules groupées par l’agrégation. Par ailleurs, il est aussi possible de spécifier d’autres fonctions pour calculer la valeur des cellules de plus grande résolution en utilisant l’option fun. Par exemple, nous pourrions choisir que la valeur agrégée corresponde à la valeur maximum des valeurs des cellules groupées.
T_fact4_moy <- aggregate(T_sec, fact = 4)
T_fact4_max <- aggregate(T_sec, fact = 4, fun = 'max')
T_fact8_moy <- aggregate(T_sec, fact = 8)
T_fact8_max <- aggregate(T_sec, fact = 8, fun = 'max')
mapviewOptions(basemaps = "OpenStreetMap")
map_fact4_moy <- mapview(T_fact4_moy, legend = FALSE, homebutton = FALSE)
map_fact4_max <- mapview(T_fact4_max, legend = FALSE, homebutton = FALSE)
map_fact8_moy <- mapview(T_fact8_moy, legend = FALSE, homebutton = FALSE)
map_fact8_max <- mapview(T_fact8_max, legend = FALSE, homebutton = FALSE)
leafsync::latticeView(map_fact4_moy, map_fact4_max, map_fact8_moy, map_fact8_max, ncol = 2)Remarquez que nous avons utilisé la fonction latticeView() pour visualiser ces quatre cartes sur deux colonnes.
5.1.8 Changer la projection d’un raster
Comme pour les données vectorielles, il est possible de manipuler le système de coordonnées de référence de données matricielles. Rappelons que pour connaître le SCR d’un raster il s’agit d’utiliser la fonction crs() de la bibliothèque raster.
crs(T_vdq)Coordinate Reference System:
Deprecated Proj.4 representation:
+proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=46
+lat_2=60 +x_0=0 +y_0=0 +datum=NAD83 +units=m
+no_defs
WKT2 2019 representation:
PROJCRS["unknown",
BASEGEOGCRS["unknown",
DATUM["North American Datum 1983",
ELLIPSOID["GRS 1980",6378137,298.257222101,
LENGTHUNIT["metre",1]],
ID["EPSG",6269]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8901]]],
CONVERSION["unknown",
METHOD["Lambert Conic Conformal (2SP)",
ID["EPSG",9802]],
PARAMETER["Latitude of false origin",44,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8821]],
PARAMETER["Longitude of false origin",-68.5,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8822]],
PARAMETER["Latitude of 1st standard parallel",46,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8823]],
PARAMETER["Latitude of 2nd standard parallel",60,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8824]],
PARAMETER["Easting at false origin",0,
LENGTHUNIT["metre",1],
ID["EPSG",8826]],
PARAMETER["Northing at false origin",0,
LENGTHUNIT["metre",1],
ID["EPSG",8827]]],
CS[Cartesian,2],
AXIS["(E)",east,
ORDER[1],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]],
AXIS["(N)",north,
ORDER[2],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]]] Nous pouvons également utiliser la fonction st_crs() de la bibliothèque sf sur un raster. Cela nous permet d’obtenir, entre autres, le SCR selon la syntaxe PROJ4.
library(sf)
st_crs(T_vdq)$proj4string[1] "+proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=46 +lat_2=60 +x_0=0 +y_0=0 +datum=NAD83 +units=m +no_defs"Rappelons que les arguments de la notation PROJ4 ont la signification suivante:
+proj: le nom de la projection+lat_0: la latitude de l’origine+lon_0: la longitude du méridien central+lat_1: la latitude du premier parallèle standard35+lat_2: la latitude du deuxième parallèle standard+x_0: le faux est (false easting; dans le cas de projection transverse comme UTM)+y_0: le faux nord (false northing)+datum: le nom du datum+units: les unités (mètres, pieds, etc.)
Nous remarquons que les données matricielles sur les îlots de chaleur de la ville de Québec sont dans la projection conique conforme de Lambert (+proj=lcc). Cette dernière est appropriée pour représenter des données à l’échelle de la province. Celle-ci est basée sur le datum NAD83 qui est très proche du datum WGS84. Retournez voir le Module 2 pour un rappel des systèmes de coordonnées de référence!
Nous voulons maintenant transformer le système de coordonnées de référence du raster T_vdq vers le système MTM, c’est-à-dire la projection Mercator transverse modifiée. Celle-ci est basée aussi sur le datum NAD83. Dans le système MTM, la ville de Québec se situe dans le fuseau 7.
Pour savoir comment définir cette projection, c’est-à-dire quels paramètres utilisés, vous pouvez vous rendre sur le site web spatialreference.org. Dans la fenêtre de recherche Search tapez “MTM zone 7”. Une liste de code EPSG apparaîtra. Sélectionnez le code “EPSG:2949: NAD83(CSRS) / MTM zone 7”. Le carré gris qui apparaît propose différents formats possibles pour définir une projection. Choisissez “Proj4”. La liste des paramètres qui définissent la projection MTM pour le fuseau 7 est alors donnée. Vous pouvez donc copier cette définition, et l’utiliser pour définir la nouvelle projection.
proj_mtm7 <- "+proj=tmerc +lat_0=0 +lon_0=-70.5 +k=0.9999 +x_0=304800 +y_0=0 +ellps=GRS80 +units=m +no_defs"Pour transformer la projection d’un raster, nous devons utiliser la fonction projectRaster() de la bibliothèque Raster.
T_mtm7 <- projectRaster(T_vdq, crs = proj_mtm7)Comparons les deux cartes utilisant des projections différentes:
par(mfrow = c(1,2))
plot(T_vdq, main = "Québec Lambert", legend = FALSE)
plot(T_mtm7, main = "MTM fuseau 7")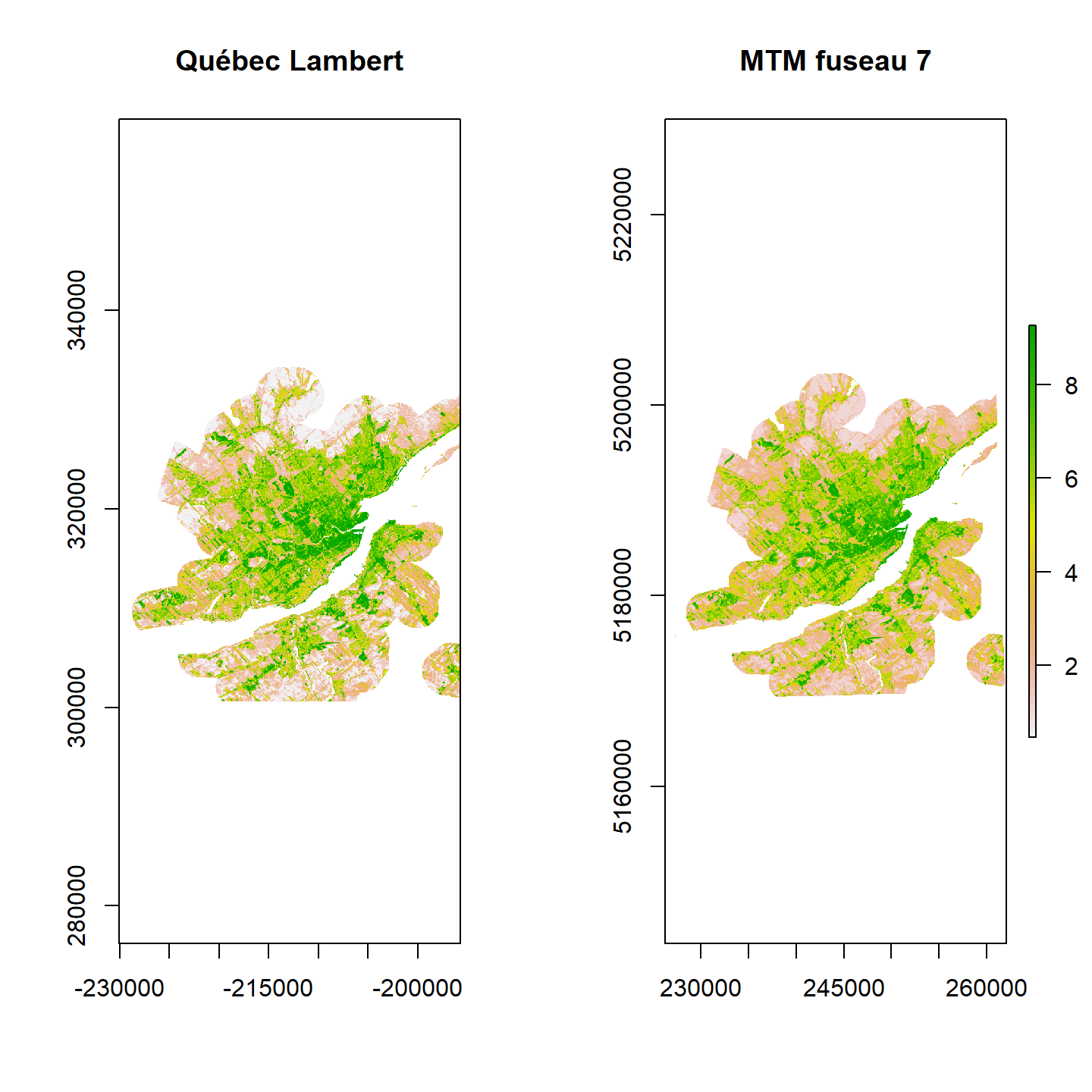
FIGURE 5.13: Rasters de projections Québec Lambert et MTM
Il est difficile de percevoir une différence, car celle-ci est légère. Pour s’en convaincre, visualisons une plus petite section de la carte de la ville de Québec:
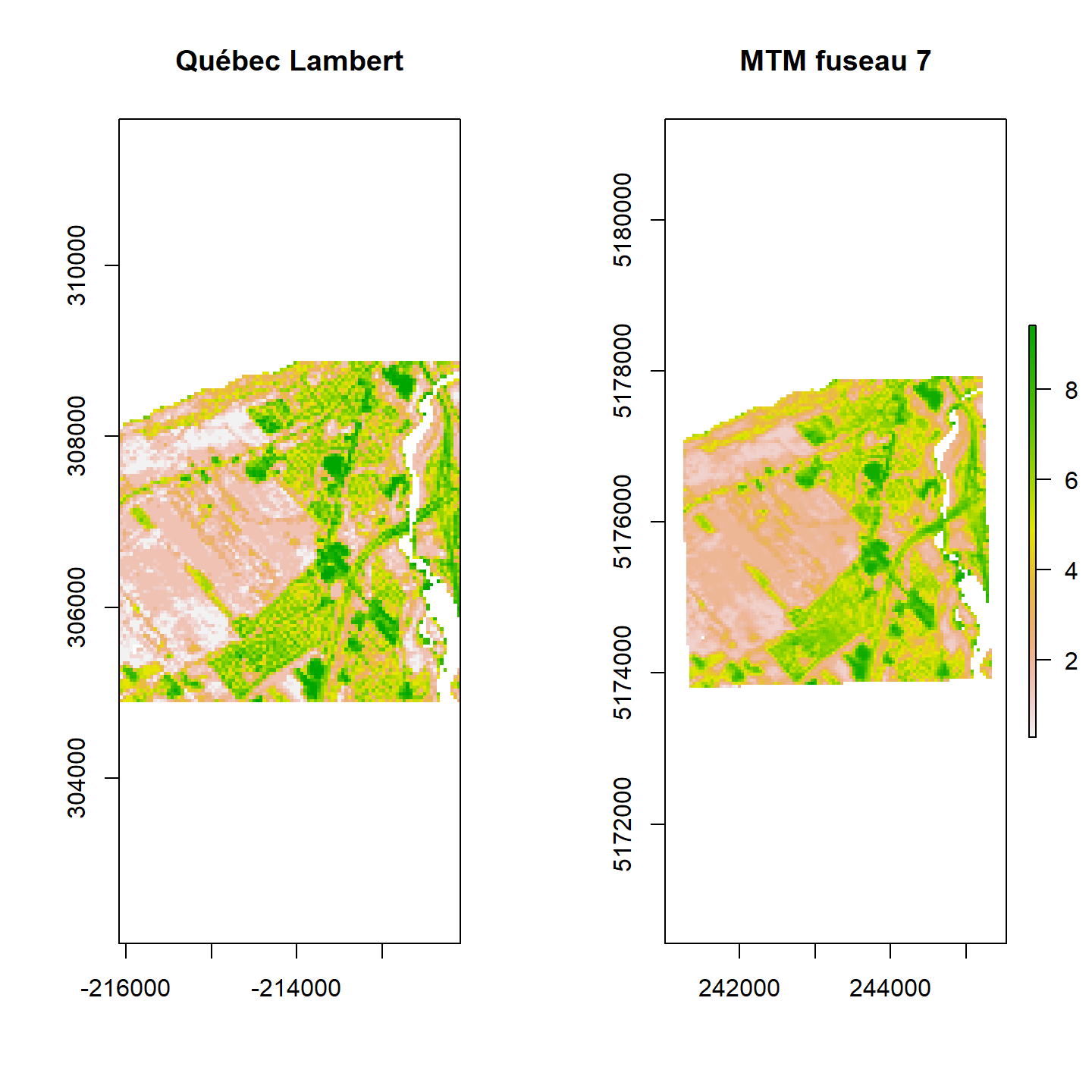
FIGURE 5.14: Section des rasters de projections Québec Lambert et MTM
Remarquez que la carte de droite, utilisant la projection MTM, est, en effet, inclinée par rapport à la carte utilisant la projection Québec Lambert. Remarquez aussi que les coordonnées des axes x et y sont différentes.
De plus, vous aurez sans doute remarqué que nous avons utilisé la fonction plot() et non mapview() pour afficher ces cartes. En effet, au moment d’écrire ces lignes, la fonction mapview() ne permet pas d’afficher des données matricielles dans leur CRS d’origine. Les données matricielles sont automatiquement transformées selon la projection Web de Mercator au moment de la visualisation, si bien qu’il est impossible de percevoir les différences provenant de projections différentes. Ce problème n’existe pas pour les données vectorielles pour lesquelles nous pouvons utiliser l’option crs.native = TRUE.
Pour sélectionner une région précise dans un raster, nous avons utilisé la fonction crop(). Nous reviendrons en détail sur cette fonction dans le module 8 qui traite de la manipulation de données matricielles.
5.1.9 Sauvegarder un raster
Finalement, pour sauvegarder des données matricielles, nous utilisons la fonction writeRaster() de la bibliothèque raster. Par exemple, sauvegardons les données matricielles T_vdq que nous avons transformées dans le système de projection MTM.
nom_du_fichier<- "Module5/Module5_donnees/ICU_vdq_MTM7.tif"
writeRaster(T_mtm7,nom_du_fichier)5.1.10 Lire et visualiser des données matricielles multi-bande
Les données matricielles peuvent contenir plusieurs couches, appelées aussi des bandes ou des canaux. C’est le cas des images de couleurs qui contiennent souvent trois bandes: une bande de rouge, une bande de vert et une bande de bleu. Dans cette section, nous apprendrons à lire et visualiser ce type de raster en utilisant des données satellitaires.
Le gouvernement québécois abrite sur son site Données Québec les données satellites, captées par Sentinel-2 et Landsat, couvrant l’ensemble de la province. Nous parlons alors d’une mosaïque d’images. Sentinel-2 est une mission d’observation de la Terre de l’Agence spatiale européenne, tandis que Landsat est une mission développée par l’Agence spatiale américaine. Pour en apprendre davantage sur ces programmes d’observation et sur les satellites utilisés, consultez les sites de Sentinel-2 et de Landsat ou encore les sites respectifs de Wikipédia (Sentinel-2 et Landsat).
La résolution des images captées par Sentinel-2 est de 10 m par 10 m, et celle de Landsat est de 30 m par 30 m. Ces images permettent ainsi d’identifier la couverture du sol avec beaucoup de précisions. On les utilise alors pour décrire comment les milieux forestiers, agricoles, humides et anthropisés sont distribués sur le territoire et comment ils évoluent dans le temps. Ces images sont utilisées lors de la planification et l’aménagement du territoire et de ses ressources.
Lire des données multi-bande
Nous allons maintenant lire le fichier Landsat_LaTuque.tif qui correspond aux données satellitaires captées par Landsat sur une section du territoire de la Haute Mauricie, près de la ville de La Tuque. Pour ce faire, nous utilisons la fonction raster() de la bibliothèque `raster’:
S <- raster("Module5/Module5_donnees/Landsat_LaTuque.tif")
Sclass : RasterLayer
band : 1 (of 3 bands)
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : Landsat_LaTuque.tif
names : Landsat_LaTuque_1
values : 0, 254.8 (min, max)Nous remarquons qu’une information supplémentaire est apparue dans la description du raster. Il s’agit de band : 1 (of 3 bands).
Cette information nous précise que nous venons de lire une seule bande alors que ces données matricielles en contiennent trois. Lorsque nous rencontrons un raster de plusieurs bandes, il faut plutôt utiliser la fonction brick() ou la fonction stack() de la bibliothèque raster pour lire l’ensemble des bandes.
S_mult <- brick("Module5/Module5_donnees/Landsat_LaTuque.tif")Remarquez que la classe de l’objet S_mult est RasterBrick et non pas simplement Raster comme l’objet S précédent. De plus, dimensions spécifie maintenant que S_mult contient trois couches (nlayers). Le nom de chaque couche est également donné: Landsat_LaTuque.1, Landsat_LaTuque.2 et Landsat_LaTuque.3. Finalement, les valeurs minimum (0) et maximum (255) sont données pour chacune des trois couches.
Nous pouvons sélectionner chacune des bandes à partir du raster multi-bande de la façon suivante:
SR <- S_mult$Landsat_LaTuque_1
SG <- S_mult$Landsat_LaTuque_2
SB <- S_mult$Landsat_LaTuque_3Par ailleurs, nous pouvons également lire chacune des bandes individuellement avec la fonction raster():
nom_fichier <- "Module5/Module5_donnees/Landsat_LaTuque.tif"
SR <- raster(nom_fichier, band = 1) #lecture de la bande rouge
SG <- raster(nom_fichier, band = 2) #lecture de la bande verte (green)
SB <- raster(nom_fichier, band = 3) #lecture de la bande bleu
SR
class : RasterLayer
band : 1 (of 3 bands)
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : Landsat_LaTuque.tif
names : Landsat_LaTuque_1
values : 0, 254.8 (min, max)
SG
class : RasterLayer
band : 2 (of 3 bands)
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : Landsat_LaTuque.tif
names : Landsat_LaTuque_1
values : 2, 255 (min, max)
SB
class : RasterLayer
band : 3 (of 3 bands)
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : Landsat_LaTuque.tif
names : Landsat_LaTuque_1
values : 0, 254.8 (min, max)Ainsi, SR correspond à la première bande (la rouge), SG à la deuxième bande (la verte), et SB à la troisième bande (la bleu). Chaque raster comprend des valeurs entre 0 et 255. Ces valeurs correspondent au format RGB, et ensemble ces trois couches permettent de visualiser des images couleurs.
RasterBrick et RasterStack
Un RasterBrick correspond généralement à différentes bandes spectrales stockées dans un seul objet ou un seul fichier dans la mémoire de votre ordinateur.
D’autre part, un RasterStack qu’on obtient par l’utilisation de la fonction stack() permet de combiner des couches provenant de fichiers différents ou d’objets logés à différents endroits de la mémoire de votre ordinateur. Une condition essentielle pour combiner des couches dans un RasterStack est que celles-ci possèdent la même étendue, la même résolution, et le même SCR.
Démontrons en quoi consiste unRasterStack par un exemple. Définissons deux couches provenant d’objets différents que nous combinerons par l’utilisation de la fonction stack().
D’abord, utilisons la fonction raster() pour créer un raster qui possède la même géométrie que les couches du raster S_mult.
raster_1 <- raster(res = res(SR), ext = extent(SR), crs = crs(SR))Attribuons des valeurs aux pixels de raster_1. Par exemple,
values(raster_1) = 1:ncell(SR)Ici, chaque pixel a comme valeur le numéro de son indice dans la matrice.
Ensuite, définissons un deuxième couche correspondant à une bande du raster S_mult:
raster_2 <- SRRemarquez que la source de chaque couche ainsi créée diffère:
raster_1class : RasterLayer
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : memory
names : layer
values : 1, 63001 (min, max)raster_2class : RasterLayer
band : 1 (of 3 bands)
dimensions : 251, 251, 63001 (nrow, ncol, ncell)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
source : Landsat_LaTuque.tif
names : Landsat_LaTuque_1
values : 0, 254.8 (min, max)Maintenant, combinons ces deux couches pour former un RasterStack en utilisant la fonction stack():
R_stack <- stack(raster_1, raster_2)
R_stackclass : RasterStack
dimensions : 251, 251, 63001, 2 (nrow, ncol, ncell, nlayers)
resolution : 60, 60 (x, y)
extent : -483210, -468150, 462630, 477690 (xmin, xmax, ymin, ymax)
crs : +proj=lcc +lat_0=44 +lon_0=-68.5 +lat_1=60 +lat_2=46 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs
names : layer, Landsat_LaTuque_1
min values : 1, 0
max values : 63001.0, 254.8 Nous avons ainsi créé un raster de classe RasterStack.
Visualiser un raster multi-bande
Visualisons individuellement les bandes d’un raster multi-bande en utilisant la fonction mapview() de la bibliothèque mapview.
# Définissons une palette de gris de 256 tons différents
mapviewOptions(raster.palette = gray.colors(256))
# Créons une carte pour chaque bande
Map_SR <- mapview(SR, homebutton = FALSE)
Map_SG <- mapview(SG, homebutton = FALSE)
Map_SB <- mapview(SB, homebutton = FALSE)
# Visualisons les trois cartes côte à côte
leafsync::latticeView(Map_SR, Map_SG, Map_SB, ncol = 3)Nous pouvons également visualiser les trois bandes ensemble en utilisant la fonction viewRGB() de la bibliothèque mapview. Cette fonction s’applique au raster multibande, et demande qu’on spécifie quelle couche du raster est associée à chacune des couleurs rouge, vert et bleu.
viewRGB(S_mult, r = 1, g = 2, b = 3)Les diverses teintes observées sur l’image Landsat peuvent être interprétées pour déduire le type de végétation ou d’utilisation du sol présent. Par exemple, les teintes de vert varient selon l’âge d’un peuplement forestier, sa densité, et s’il est composé de feuillus ou de conifères. Les teintes roses, brunes ou bourgognes sont associées à des perturbations, comme des épidémies d’insecte ou des feux de forêt. Ici, les pixels roses signalent la présence de coupes forestières36.
Finalement, pour sauvegarder un raster multibande, nous pouvons encore utiliser la fonction writeRaster() de la bibliothèque raster.
writeRaster(S_mult, "Module5/Module5_donnees/LaTuque-copie.tif")Si vous désirez comprendre la méthodologie utilisée pour déterminer la température de surface à partir d’images satellitaires, consulter cette note technique produite par le Centre d’enseignement et de recherche en foresterie de Sainte-Foy inc.↩︎
OpenStreetMap est un outil collaboratif et libre d’accès de cartographie en ligne.↩︎
Souvenez-vous que pour une projection cylindrique ou conique, le plan intersecte le globe le long d’un ou de deux parallèles. Voir la leçon 2↩︎
Pour plus d’informations sur l’interprétation des images Landsat, consultez ce guide produit par le Ministère des Forêts, de la Faune et des Parcs du Québec (Direction des inventaires forestiers 2015).↩︎